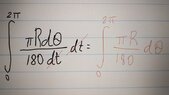Is It Possible? Solving Calculus Questions with Ease

  • Context: Undergrad 
  • Thread starter Thread starter NODARman
  • Start date Start date
  • Tags Tags
    Calculus
Click For Summary
SUMMARY

The discussion centers on the nuances of calculus, specifically the treatment of derivative notation such as ##\dfrac{d \theta }{dt}##. It is established that while this notation resembles a fraction, it is not mathematically valid to cancel the dt's. Instead, the chain rule illustrates how to manipulate these derivatives correctly, as shown in the equation ##\dfrac{d \theta }{dx} = \dfrac{d \theta }{dt} \cdot \dfrac{dt}{dx}##. Additionally, when integrating with respect to t, the bounds must be adjusted accordingly to ##\int_{t(0)}^{t(2\pi)}##.

PREREQUISITES
  • Understanding of calculus concepts, particularly derivatives and integrals.
  • Familiarity with the chain rule in calculus.
  • Knowledge of differential notation and its applications.
  • Basic skills in manipulating mathematical expressions and equations.
NEXT STEPS
  • Study the implications of the chain rule in calculus.
  • Learn about differential notation and its historical context in mathematics.
  • Explore advanced integration techniques and their applications.
  • Investigate the concept of limits and their role in calculus.
USEFUL FOR

Students, educators, and professionals in mathematics or engineering fields who seek to deepen their understanding of calculus and its practical applications.

NODARman
Messages
57
Reaction score
13
TL;DR
.
Hi, just wondering if that's possible in calculus.
(See the attachment)
 

Attachments

  • 166920054969935055318737542524.jpg
    166920054969935055318737542524.jpg
    37.6 KB · Views: 179
Physics news on Phys.org
NODARman said:
TL;DR Summary: .

Hi, just wondering if that's possible in calculus.
(See the attachment)
What you wrote was essentially correct. But...

In reality? No. The derivative notation ##\dfrac{d \theta }{dt}## is not actually a fraction so you cannot cancel the dt's.

However, in practice you can "cancel" the dt's. It's a similar effect to the chain rule: ##\dfrac{d \theta }{dx} = \dfrac{d \theta }{dt} \cdot \dfrac{dt}{dx}##. Again, there is no real cancellation, but it appears that way.

Mathematicians in the 1800s spent a great deal of time showing how you can treat a differential element as a fraction. Most of the time you can get away with it.

-Dan
 
Reply
  • Like
Likes   Reactions: scottdave, DaveE, vela and 1 other person
Technically the bounds on the integral need to change to ##\int_{t(0)}^{t(2\pi)}## if you are integrating wrt ##t##.
 
Reply
  • Like
Likes   Reactions: DaveE and topsquark

Similar threads

Undergrad I want to know which software was used to create vector calculus graph
  • · Replies 2 ·
Replies
2
Views
2K
MHB Question about the differential in Calculus
  • · Replies 9 ·
Replies
9
Views
2K
High School Question about the fundamental theorem of calculus
  • · Replies 2 ·
Replies
2
Views
3K
Undergrad Calculus of Variations on Kullback-Liebler Divergence
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Have you ever used "symbolic logic" to help you learn calculus?
  • · Replies 5 ·
Replies
5
Views
2K
High School Some questions while I self-learn Applied Calculus
  • · Replies 49 ·
2
Replies
49
Views
7K
Undergrad Should the function f to be continuous for applying MVTI or not?
  • · Replies 4 ·
Replies
4
Views
1K
Undergrad What would a calculus author have to say on ##\int r^2dm##?
  • · Replies 11 ·
Replies
11
Views
3K
High School Vertical asymptote with an epsilon-delta proof?
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Analysis of functions of a single variable via multivariable calculus?
  • · Replies 10 ·
Replies
10
Views
2K