Discussion Overview
The discussion revolves around the simplification of multivariable limits, particularly focusing on a limit involving two variables, x and a, along with a constant n. Participants explore algebraic manipulations and the application of L'Hôpital's rule in the context of evaluating the limit.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant expresses difficulty with a limit involving two variables and shares their initial algebraic manipulation.
- Another participant questions the identification of the variable in the limit, suggesting that only x is changing while a and n are constants.
- A participant attempts to factor out (x-a) from the numerator and discusses the challenges faced in simplifying the expression further.
- There is a correction regarding the factorization of x^n - a^n, with one participant asserting that it does not equal (x-a)(x^{n-1} - a^{n-1}) and providing the correct factorization.
- Another participant confirms the correction and reiterates the proper factorization of x^n - a^n.
- A participant acknowledges confusion regarding different formatting protocols used in the forum.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the simplification process, with multiple viewpoints on the correct factorization and the nature of the variables involved. Disagreement exists regarding the algebraic manipulations and interpretations of the limit.
Contextual Notes
There are unresolved assumptions regarding the treatment of variables and constants in the limit, as well as the steps involved in the algebraic simplification.
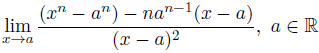
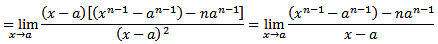 ,
,