Discussion Overview
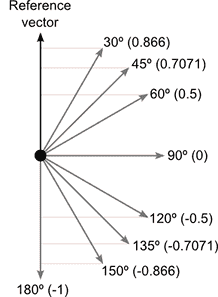
The discussion revolves around the possibility of customizing the dot product to yield linear outputs based on angles, specifically aiming for values like 0.5 at 45 degrees, 0.33 at 60 degrees, and 0.66 at 30 degrees. Participants explore the implications of redefining the dot product and its mathematical properties.
Discussion Character
- Debate/contested
- Technical explanation
- Conceptual clarification
Main Points Raised
- One participant questions the feasibility of making the dot product change linearly, suggesting that such a redefinition would not retain the properties of the dot product.
- Another participant explains that the dot product between two unit vectors is defined as ##\cos(\theta)## and proposes calculating the angle using the inverse cosine function, which can then be scaled.
- A later reply emphasizes the importance of the unit vector condition for the relationship between the dot product and cosine to hold true, suggesting that a different approach, like a switch statement or class, might be more appropriate for the desired functionality.
- There is a repeated acknowledgment of the relationship between the dot product and cosine, with one participant expressing surprise at this connection.
Areas of Agreement / Disagreement
Participants express differing views on the feasibility and implications of redefining the dot product. There is no consensus on how to achieve the desired linearity while maintaining the mathematical integrity of the dot product.
Contextual Notes
Participants highlight the necessity of unit vectors for the standard definition of the dot product and suggest that any redefinition may lead to a loss of its conventional properties.