Undergrad Can this method be used to prove the Collatz Conjecture?

[Dtriction]

There is a graph showing n on its x-axis and its total stopping time on its y axis.

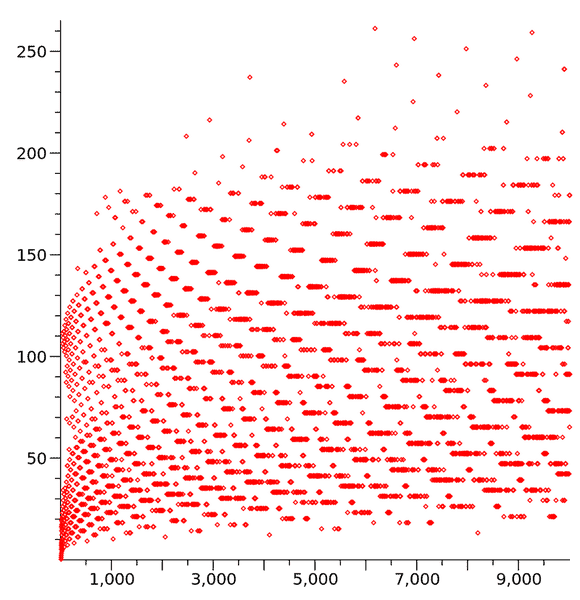
From here we can see that the points on the graph are not random at all; they have some kind of geometric pattern that is due to the 3x+1 in the odd case and x/2 in the even case. I have seen many attempts to prove the Collatz Conjecture but all that I have seen do not make any reference to the geometric patterns in the above graph. What if we work on establishing how the two cases' formulae relate to the above graph's geometric patterns and then extrapolate it? Might it be possible to find out something new from the formulae that would be really not apparent without this graph? Wouldn't it transform the original conjecture into a geometric problem, a new way of looking at it which may provide fresh new insights?

This method should work not for just the Collatz Conjecture,if I guess correctly. A math problem that could be graphed in some way would turn it into geometric problems which then could be solved/used to obtain new insights by geometry,wouldn't it?

 

[fresh_42]

Symmetries of the Collatz conjecture are not unknown. Of course such graphics might be useful as an inspiration, but I think not for very much more. Assuming there is no counterexample (based on the many algorithmic hours on uncounted distributed computers), and if you will, also supported by the symmetries you mentioned, the real problem is to find a proof. Experience tells us, that such a proof can lead us far away from the original formulation of the problem, and it might need a genius like Andrew Wiles or Grigori Perelman and surely many years of research, to come up with a proof.

Since I don't know such a genius, I stick with Richard Kenneth Guy: "Don’t try to solve these problems!" American Mathematical Monthly 90, 1983, p. 35–41.

 

[mfb]

All the mathematical relations correspond to some aspects of this graph, but with numbers instead of "this pattern here, no not this, that one", because proofs need to be unambiguous.

 

[fresh_42]

I think that this post here would fit in well:
https://www.physicsforums.com/threa...ithm-approximation-works.895491/#post-5633386