Discussion Overview
The discussion revolves around the methodology for finding gradients using coordinates, specifically the appropriateness of using the point of tangency versus points further away. Participants explore the implications of different approaches in the context of teaching and practical application.
Discussion Character
- Debate/contested
- Conceptual clarification
- Technical explanation
Main Points Raised
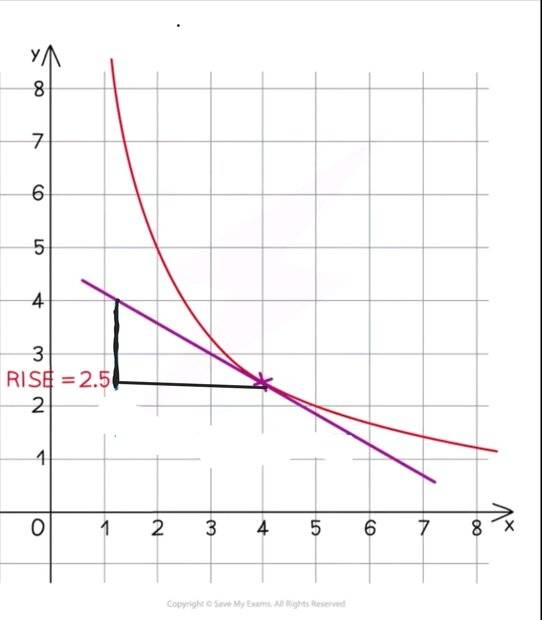
- Some participants express confusion over the difference between using the point of tangency and points further away, noting that both methods yield the same answer.
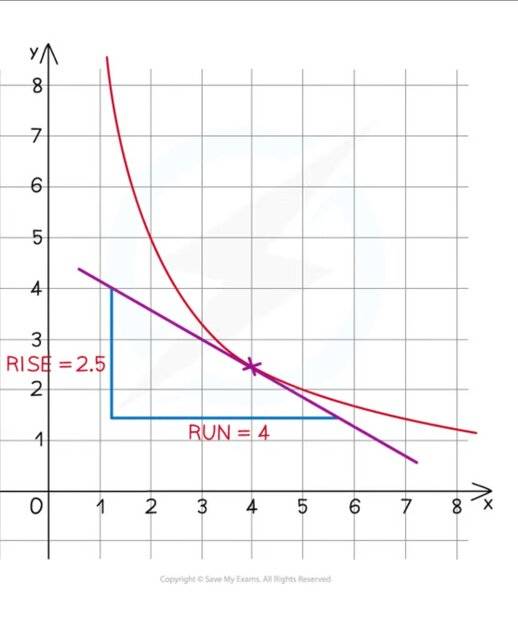
- Others argue that using the point of tangency increases the margin for error and that it is better practice to take points further away from the tangent.
- A participant suggests that the practice of excluding the point of tangency is taught to minimize uncertainty in the gradient calculation.
- Some participants question the rationale behind the teaching methods, suggesting that they may prioritize exam performance over practical understanding.
- There is a suggestion that in a freehand graph, it may be acceptable to use one point from the point of tangency and another from further away.
- One participant emphasizes the importance of constructing a larger triangle for gradient calculations to reduce uncertainty.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the best method for finding gradients. There are competing views regarding the use of the point of tangency and the implications for accuracy and teaching practices.
Contextual Notes
Participants note that the choice of coordinates can affect the uncertainty in gradient calculations, but they do not resolve the underlying assumptions or the reasons for differing teaching methods.