cgrie
- 8
- 4
- TL;DR
- Probably a better question is:
1. Can you take a derivative of an object other than a number or point and "spit out" the same type of object (i.e. same amount of elements, same types of elements)?
2. What are some examples of objects you can combine integers (i.e. factorials) with?
3. Are there any operations other than addition that are neat to look at?
I was recently studying the pressure gradient force, and I found it interesting (though this may be incorrect) that you can use a Taylor expansion to pretend that the value of the internal pressure of the fluid does not matter at all, because the internal pressure forces that are a part of the pressure on opposing sides seem to cancel out.
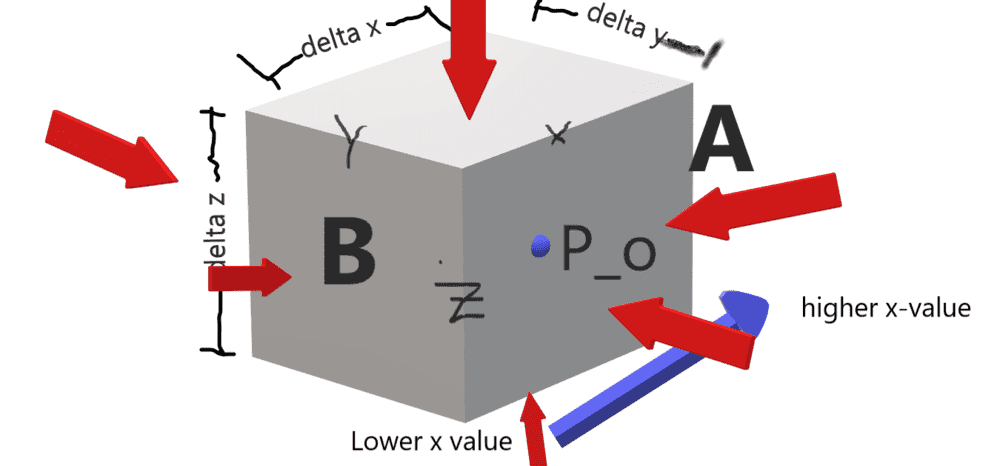
Suppose the internal pressure of the infinitesimal fluid is: ##p_0 = p(x_0,y_0,z_0)## where ##x_0,y_0,z_0## are all constants.
Thus, the total pressure on any side is ##p_0 + p_{out}##.
Thus, for pressures on the axis:
$$p_{Ax}=p_0 + \frac{\partial p}{\partial x}\frac{\delta x}{2} + \text{Higher order terms}$$
And for the opposing direction :
$$p_{Bx}=p_0 - \frac{\partial p}{\partial x}\frac{\delta x}{2} + \text{Higher order terms}$$
We will ignore the higher order terms. (The book says so, but how important is this?)
Then, if we multiply the pressure by the area of the side the pressure acts on, as well as multiplying by the direction toward the center (from the respective side, we get the forces:
$$F_{Ax} = -(p_0 + \frac{\partial p}{\partial x}\frac{\delta x}{2})\delta y \delta z$$
$$F_{Bx} = (p_0 - \frac{\partial p}{\partial x}\frac{\delta x}{2})\delta y \delta z$$
Thus,
$$F_{Ax} + F_{Bx} = -\frac{\partial p}{\partial x}\delta x \delta y \delta z$$
The internal pressures cancel, which makes sense in ##\mathbb{R}^3## (It seems to make sense in ##\mathbb{R}^4,\mathbb{R}^5##, etc.
But what if we don't use numbers and use something like sets?
Hypothetically if you define ##p_0## to be a set (like ##\mathbb{Z}##), then subtracting the internal "pressures"
will yield an empty set rather than 0. If you concatenate a null set with any set, this would seem to work, But of course this is broken math and an abuse of notation because subtraction of numbers is negative addition, and the difference of sets ##S_1-S_2## is the elements of ##S_1## not in ##S_2##.
It seems like to reverse a difference of the sets, you can do ##(S_1-S_2)\cup{S_2}## , which involves concatenation. However, I am not sure if concatenation of any 2 sets is necessarily the inverse of a difference of the same two sets for a variety of reasons like:
a) If ##S_1## and ##S_2## are disjoint, ##S_1-S_2## is ##S_1## , also ##(S_1-S_2) \cup{S_2}## is ##S_1\cup{S_2}## I'm not sure if not concatenating is an inverse of concatenating.
With this in mind, are there types of operations that modify individual elements (like addition, etc.) as well as modify completely different elements at the same time, while still retaining the definition?
Side note: what are some applications of Taylor series other than estimation of differentiable functions? (I copied a picture from a textbook called Mid-Latitude Atmospheric Dynamics by Martin, for reference)
Forces (red) are orthogonal to the planes of the sides
Thank you so much!
Suppose the internal pressure of the infinitesimal fluid is: ##p_0 = p(x_0,y_0,z_0)## where ##x_0,y_0,z_0## are all constants.
Thus, the total pressure on any side is ##p_0 + p_{out}##.
Thus, for pressures on the axis:
$$p_{Ax}=p_0 + \frac{\partial p}{\partial x}\frac{\delta x}{2} + \text{Higher order terms}$$
And for the opposing direction :
$$p_{Bx}=p_0 - \frac{\partial p}{\partial x}\frac{\delta x}{2} + \text{Higher order terms}$$
We will ignore the higher order terms. (The book says so, but how important is this?)
Then, if we multiply the pressure by the area of the side the pressure acts on, as well as multiplying by the direction toward the center (from the respective side, we get the forces:
$$F_{Ax} = -(p_0 + \frac{\partial p}{\partial x}\frac{\delta x}{2})\delta y \delta z$$
$$F_{Bx} = (p_0 - \frac{\partial p}{\partial x}\frac{\delta x}{2})\delta y \delta z$$
Thus,
$$F_{Ax} + F_{Bx} = -\frac{\partial p}{\partial x}\delta x \delta y \delta z$$
The internal pressures cancel, which makes sense in ##\mathbb{R}^3## (It seems to make sense in ##\mathbb{R}^4,\mathbb{R}^5##, etc.
But what if we don't use numbers and use something like sets?
Hypothetically if you define ##p_0## to be a set (like ##\mathbb{Z}##), then subtracting the internal "pressures"
will yield an empty set rather than 0. If you concatenate a null set with any set, this would seem to work, But of course this is broken math and an abuse of notation because subtraction of numbers is negative addition, and the difference of sets ##S_1-S_2## is the elements of ##S_1## not in ##S_2##.
It seems like to reverse a difference of the sets, you can do ##(S_1-S_2)\cup{S_2}## , which involves concatenation. However, I am not sure if concatenation of any 2 sets is necessarily the inverse of a difference of the same two sets for a variety of reasons like:
a) If ##S_1## and ##S_2## are disjoint, ##S_1-S_2## is ##S_1## , also ##(S_1-S_2) \cup{S_2}## is ##S_1\cup{S_2}## I'm not sure if not concatenating is an inverse of concatenating.
With this in mind, are there types of operations that modify individual elements (like addition, etc.) as well as modify completely different elements at the same time, while still retaining the definition?
Side note: what are some applications of Taylor series other than estimation of differentiable functions? (I copied a picture from a textbook called Mid-Latitude Atmospheric Dynamics by Martin, for reference)
Forces (red) are orthogonal to the planes of the sides
Thank you so much!