Car crash conservation of momentum problem

[BrainMan]

Homework Statement

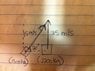
A 2200-kg van traveling north along the interstate at 25 m/s is involved in a perfectly inelastic collision with a 1500-kg automobile driven by a careless motorist who emerges at a speed of 15 m/s form an entrance ramp that makes an angle of 20 degrees with the highway. Find the magnitude and direction of the velocity of the combined wrecked vehicles.

Homework Equations

The equation for inelastic collisions

The Attempt at a Solution

What I did was find the sum of all the momentum in the x direction so
15 cos (20) * 1500 = 21143.08397
and the sum of all the momentum in the y direction so
15 sin (20) *1500 + 25(2200) = 62695.45322
and then I did tanθ = 62695.45322/21143.08397
then I did inverse tan to find theta and got 71 degrees. The correct answer is 5.78° relative to the vans original direction.

 

[Nathanael]

What I did was find the sum of all the momentum in the x direction so
15 cos (20) * 1500 = 21143.08397
and the sum of all the momentum in the y direction so
15 sin (20) *1500 + 25(2200) = 62695.45322

Draw a picture. Would it be the sine or the cosine that is the x direction?

 

[BrainMan]

Draw a picture. Would it be the sine or the cosine that is the x direction?

I am pretty sure its sine.

 

[Nathanael]

I am pretty sure its sine.

Yes it would be. But you did cosine in your calculation.

 

[BrainMan]

Yes it would be. But you did cosine in your calculation.

Sorry I meant cos. Sin is the y direction. Why would it be sin?

 

[Nathanael]

Sorry I meant cos. Sin is the y direction. Why would it be sin?

Let's make sure we're talking about the same directions. The "y" direction is the direction that the van was initially going, right? And the "x" direction is 90 degrees to that?Check out the picture I attatched.

 

[dauto]

The 25(2200) term should be added to the 15 cos (20) * 1500 component.

 

[BrainMan]

Let's make sure we're talking about the same directions. The "y" direction is the direction that the van was initially going, right? And the "x" direction is 90 degrees to that?


Check out the picture I attatched.

I actually used the total opposite of that. Look at my drawing.

 

[Nathanael]

I actually used the total opposite of that. Look at my drawing.

But the problem says, "an entrance ramp that makes an angle of 20 degrees with the highway"

In your drawing the entrance ramp and the highway make an angle of 70 degrees.

 

[BrainMan]

But the problem says, "an entrance ramp that makes an angle of 20 degrees with the highway"

In your drawing the entrance ramp and the highway make an angle of 70 degrees.

OK I see my mistake. Thanks!