Bitmap
- 4
- 1
- Homework Statement
- While driving on a road that is inclined at an angle of 10 degrees above the horizontal, Vehicle A and Vehicle B are in a head-on collision lasting for 0.071 sec Just before the collision, Vehicle A had a velocity of 21m/s and Vehicle B had a velocity of -29m/s as shown below.
The mass of Vehicle B is 1.3 times larger than the mass of Vehicle A. After the collision, the vehicles remain stuck together. You may assume that, as the collision took place, friction and drag forces are negligible in comparison to the force between the two vehicles.
What is the velocity of the two-vehicle system immediately after the collision?
- Relevant Equations
- Trig Functions (Sin, Cos, Tan)
Conservation of Momentum: M(a) + M(b) = (m(a) + m(b))*V(f)
QUESTION:
-----------
For the purposes of this problem, we will define the direction of Vehicle A's initial velocity as the positive direction:
While driving on a road that is inclined at an angle of 10 degrees above the horizontal, Vehicle A and Vehicle B are in a head-on collision lasting for 0.071 sec Just before the collision, Vehicle A had a velocity of 21m/s and Vehicle B had a velocity of -29m/s as shown below.
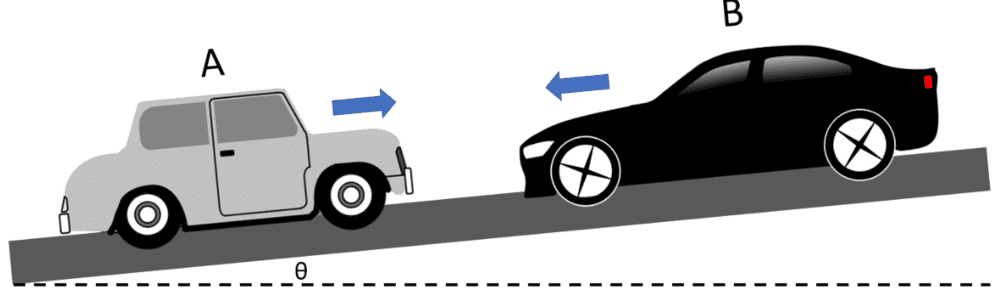
The mass of Vehicle B is 1.3 times larger than the mass of Vehicle A. After the collision, the vehicles remain stuck together. You may assume that, as the collision took place, friction and drag forces are negligible in comparison to the force between the two vehicles.
What is the velocity of the two-vehicle system immediately after the collision?
EXPLANATION/APPROACH
----------
I know that the momentum is conserved so that the total momentum when the cars are together is equal to the momentum when the cars are separate. However, I am struggling to add Trig to this equation, as I don't know whether this will provide more or less momentum, and when I should apply the formulae to solve the problem.
I can do this problem without the incline:
Momentum of A = M(a)
Mass of A = m(a)
Final Velocity = V(f)
M(a) + M(b) = (m(a) + m(b))*V(f)
From this, I can plug in the given ratios/values to come out with the final velocity.
-----------
For the purposes of this problem, we will define the direction of Vehicle A's initial velocity as the positive direction:
While driving on a road that is inclined at an angle of 10 degrees above the horizontal, Vehicle A and Vehicle B are in a head-on collision lasting for 0.071 sec Just before the collision, Vehicle A had a velocity of 21m/s and Vehicle B had a velocity of -29m/s as shown below.
The mass of Vehicle B is 1.3 times larger than the mass of Vehicle A. After the collision, the vehicles remain stuck together. You may assume that, as the collision took place, friction and drag forces are negligible in comparison to the force between the two vehicles.
What is the velocity of the two-vehicle system immediately after the collision?
EXPLANATION/APPROACH
----------
I know that the momentum is conserved so that the total momentum when the cars are together is equal to the momentum when the cars are separate. However, I am struggling to add Trig to this equation, as I don't know whether this will provide more or less momentum, and when I should apply the formulae to solve the problem.
I can do this problem without the incline:
Momentum of A = M(a)
Mass of A = m(a)
Final Velocity = V(f)
M(a) + M(b) = (m(a) + m(b))*V(f)
From this, I can plug in the given ratios/values to come out with the final velocity.