Center Gravity and Moment of Inertia

[ymehuuh]

Homework Statement

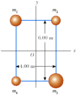
Four objects are held in position at the corners of a rectangle by light rods as shown in the figure below. The mass values are given below.
M1 (kg) M2 (kg) M3 (kg) M4 (kg)
3.50 1.50 3.90 1.70

(a) Find the moment of inertia of the system about the x axis.

(b) Find the moment of inertia of the system about the y axis.

(c) Find the moment of inertia of the system about an axis through O and perpendicular to the page.

Homework Equations

Center of Gravity: sumM1*X1+M1*X2.../M1+M2...

The Attempt at a Solution

I found the center of gravity for the x-axis to be .037736...how do I find the moment of inertia with that information?

 

[LowlyPion]

You need to find the x and y CoM.

Knowing that then the moment I about the CoM is Σmr².

The axes are simpler in that for

I_x = Σm_i*y_i²

I_y = Σm_i*x_i²

 

[ymehuuh]

Oh, I reversed the two and that's why I got it wrong. Thanks.
What would I use for part c?

 

[LowlyPion]

Oh, I reversed the two and that's why I got it wrong. Thanks.
What would I use for part c?

What are the distances to each corner from O to each mass?

I_o = Σmr²

It's made a little easier by Pythagoras, so be sure and thank him.

 

[ymehuuh]

what are the distances to each corner from o to each mass?

I_o = Σmr²

it's made a little easier by pythagoras, so be sure and thank him.

perfect! Thanks!