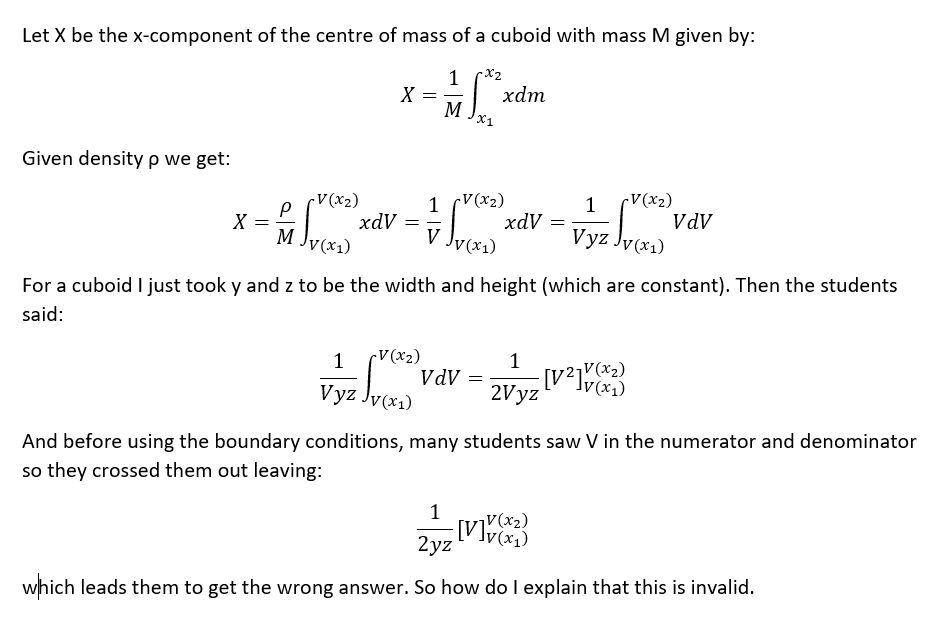Centre of Mass of a Uniform Cuboid -- Show that it is at the Center

[patrykh18]

Homework Statement:

Starting from a definition of Centre of Mass, show explicitly that for a uniform cuboid the centre of mass is at the centre.

Relevant Equations:

Provided below.

So, I volunteered to run a seminar to first year students in my college. They got a question like this for homework recently and a lot of them made a mistake in the calculation. I am not asking for help with the question itself because I know how to do it. However, a lot of students made a mistake that I shown in the image below. I'm curious about what would be the best way to explain to them why that is a wrong approach (without going into too much details about mathematics).

 

Woahhhhhh, why you putting volumes in the limits?

 

[patrykh18]

Woahhhhhh, why you putting volumes in the limits?

Well I am going from x1 to x2 but it's all multiplied by yz

 

[PeroK]

Well I am going from x1 to x2 but it's all multiplied by yz

It should be multiplied by the constant cross sectional area, surely?

 

[patrykh18]

It should be multiplied by the constant cross sectional area, surely?

Yeah yz is the constant cross area

 

I was trying to figure out how to answer this but there's too much wrong at the moment to make a start. You have $x$'s in the limits for your integration with respect to $m$, you use $V$ both as the volume of the cuboid and as an integration variable, you set $V=xyz$ at one point, when this is clearly incorrect [$x$, $y$ and $z$ are coordinates..., and I don't even know which $V$ you're trying to refer to], you have some weird limits. Too much to untangle for me, sorry.

 

[PeroK]

Yeah yz is the constant cross area

The standard approach should integrate with respect to $x$, and not $V$. In any case, you cannot have $V$ as the fixed volume of the cube and an integration variable. That's a problem that encourages the invalid cancellation.

 

[patrykh18]

I was trying to figure out how to answer this but there's too much wrong at the moment to make a start. You have $x$'s in the limits for your integration with respect to $m$, you use $V$ both as the volume of the cuboid and as an integration variable, you set $V=xyz$ at one point, when this is clearly incorrect [$x$, $y$ and $z$ are coordinates..., and I don't even know which $V$ you're trying to refer to], you have some weird limits. Too much to untangle for me, sorry.

Yeah. I solved a lot of integrals. I know I need to distinguish between $V$ the volume and $V$ the integration parameter. I just never asked myself why you fundamentally have to do it.

 

[patrykh18]

The standard approach should integrate with respect to $x$, and not $V$. In any case, you cannot have $V$ as the fixed volume of the cube and an integration variable. That's a problem that encourages the invalid cancellation.

Yeah, if I did this question I would naturally distinguish between those two but I never asked myself why that is fundamentally the case.