Finding the center of mass of a simple 2D shape

[JohnnyLaws]

Homework Statement

We have a uniform square of 15 unit of lenght and a triangular hole in it. This triangle is known to be isosceles, and the distance between the center of the square and its edge is 7,5 units, which is equivalent to the height of the triangle. I'll show the image.

Relevant Equations

I think I need to use this equation:
(∫xdA)/A
Integral limits and derivation of dA will be approached in the next section.
Essentially, I'm attempting to calculate the center of mass of the square, taking into account that the origin for the center of mass is the bottom left corner of the square, while the origin for the center of mass of the triangle is shifted 7.5 units in the x-direction and remains at y = 0 units relative to the other origin.

Here it is the image of the statement:

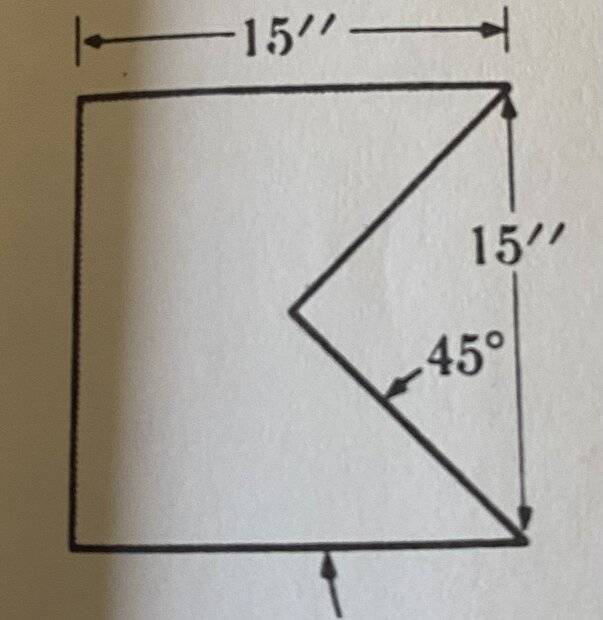
As I mentioned in the "relevant equations" section, my approach to solving this exercise involves calculating the difference between the centers of mass of the square and the triangle.

Starting with calculation of center of mass for the square.

Starting with the initial equation for the x-coordinate:

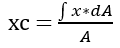
When making small changes in x (dx), we can express dA in terms of dx. In other words, we can write: dA = dx * y.

So, we can rewrite the equation for xc:

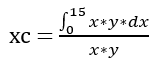
Since y in this case is a constant equal to 15, we can simplify the equation to:

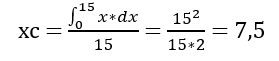Now for yc of the square:

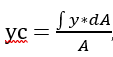
When considering a small change in y (dy), we can express dA in terms of dy. In simpler terms, we can rewrite it as: dA = dy * x

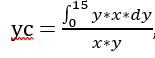
Since x in this case is a constant equal to 15, we can simplify the equation to:

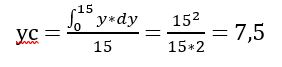
So as we expected for a homgeneous square, the center of mass is in the middle.
Therefore, xc = yc = 7.5.

I'm not certain about what needs to be done for the triangle. I'm unsure how to parametrize this figure. Am I on the right track or is everything I'm thinking incorrect?
I know that's a simple exercise but I can't find anything on internet.
By the way, the solution for this exercise from the center of the square is: xc = 2.07 and yc = 0.

 

[jbriggs444]

You seem to be missing the forest because of all the trees. The trees have you all confused as well.

Let us back up and see how you attacked the problem of finding the center of gravity for the square along its $x$ coordinate.

You are splitting the square up into vertical strips, each of incremental area $dA$ you are using these areas as weights as you add up all of the positions and divide by total weight to yield the weighted average horizontal position. Otherwise known as the horizontal center of gravity. That is:$$x_c = \int \frac{x\ dA}{A}$$

You write that the incremental area $dA$ is given by $y\ dx$. But that is not correct. It is given by $15\ dx$. You've not given a definition for $y$. You are forbidden to use it in a formula without definition.

You could have arrived at that 15 by computing $\int_0^{15} dy$. But that would just trivially give you 15 as a result and would not succeed in defining $y$. [The variable of integration is not validly in scope outside of the integral where it is used]

However, by a magic handwave, you consider $y$ to be defined as 15 and obtain the correct result of 7.5 for the horizontal centroid of the square. The same result that we could have obtained from symmetry.

The computation for the vertical center of gravity is identical shares the identical failing while yielding the correct result.Now you want to compute the center of gravity for the triangle. Let us work on its horizontal center of gravity. We will be dividing the triangle up into vertical strips with incremental area $dA$ so the horizontal center of gravity will be given by the familiar formula:$$\int_\text{left edge}^\text{right edge} \frac{x\ dA}{A}$$So we have some questions:
1. What is the x coordinate of the left edge of the triangle?
2. What is the x coordinate of the right edge of the triangle?
3. What is the incremental area of a vertical strip of width $dx$ at an $x$ coordinate of $x$?

We also have a question going forward. Suppose that you have computed the horizontal position of the center of gravity of the triangle. Knowing this result, how will you compute the horizontal position of the center of gravity of the square with the triangle cut out?

Are you striving to use the negative mass trick?

 

[Chestermiller]

Hint: Take moments of the two shapes with respect to the right edge

 

[JohnnyLaws]

1. What is the x coordinate of the left edge of the triangle?
2. What is the x coordinate of the right edge of the triangle?
3. What is the incremental area of a vertical strip of width $dx$ at an $x$ coordinate of $x$?

We also have a question going forward. Suppose that you have computed the horizontal position of the center of gravity of the triangle. Knowing this result, how will you compute the horizontal position of the center of gravity of the square with the triangle cut out?

Are you striving to use the negative mass trick?

You seem to be missing the forest because of all the trees. The trees have you all confused as well.

Let us back up and see how you attacked the problem of finding the center of gravity for the square along its $x$ coordinate.

You are splitting the square up into vertical strips, each of incremental area $dA$ you are using these areas as weights as you add up all of the positions and divide by total weight to yield the weighted average horizontal position. Otherwise known as the horizontal center of gravity. That is:$$x_c = \int \frac{x\ dA}{A}$$

You write that the incremental area $dA$ is given by $y\ dx$. But that is not correct. It is given by $15\ dx$. You've not given a definition for $y$. You are forbidden to use it in a formula without definition.

You could have arrived at that 15 by computing $\int_0^{15} dy$. But that would just trivially give you 15 as a result and would not succeed in defining $y$. [The variable of integration is not validly in scope outside of the integral where it is used]

However, by a magic handwave, you consider $y$ to be defined as 15 and obtain the correct result of 7.5 for the horizontal centroid of the square. The same result that we could have obtained from symmetry.

The computation for the vertical center of gravity is identical shares the identical failing while yielding the correct result.Now you want to compute the center of gravity for the triangle. Let us work on its horizontal center of gravity. We will be dividing the triangle up into vertical strips with incremental area $dA$ so the horizontal center of gravity will be given by the familiar formula:$$\int_\text{left edge}^\text{right edge} \frac{x\ dA}{A}$$So we have some questions:
1. What is the x coordinate of the left edge of the triangle?
2. What is the x coordinate of the right edge of the triangle?
3. What is the incremental area of a vertical strip of width $dx$ at an $x$ coordinate of $x$?

We also have a question going forward. Suppose that you have computed the horizontal position of the center of gravity of the triangle. Knowing this result, how will you compute the horizontal position of the center of gravity of the square with the triangle cut out?

Are you striving to use the negative mass trick?

For the first two questions. Are you asking me relative to what referencial? If you are talking about the first referencial the x coordinate of the left edge is equal 7,5 and the right is equal to 15. If you are talking about the referencial in center of square but the y coordinate is in the base, the x coordinate of left will be 0 and right is 7,5. I don't know how to derivate the incremental area.
Yes I'm trying to use the negative mass trick

 

[jbriggs444]

For the first two questions. Are you asking me relative to what referencial?

Pick a coordinate system and use it. It seems that you have used the lower left corner of the square as your origin so far. You could continue to use that. That would be handy since your computed center of mass for the triangle would be in the same coordinate system you used for the square.

Or you could shift to a different coordinate system. For instance, one with its origin at the left hand corner of the triangle (which is also the center of the square). That would likely make the horizontal integral easier to evaluate. But it would mean that your triangle center of mass would be in a different coordinate system from your square's center of mass.

Either choice will work.

If you are talking about the first referencial the x coordinate of the left edge is equal 7,5 and the right is equal to 15.

OK, that sounds right.

If you are talking about the referencial in center of square but the y coordinate is in the base, the x coordinate of left will be 0 and right is 7,5.

The $y$ coordinate is irrelevant when evaluating the horizontal center of mass. It would be relevant when evaluating the vertical center of mass. But an argument from symmetry immediately reveals where the vertical center must be.

I don't know how to derivate the incremental area.

Remember that the incremental area is a strip that is $dx$ in width. Its height is enough to go from the top of the triangle (at the position of the strip) to the bottom. If you had a formula for that top to bottom height, you could compute $dA = \text{height at position x} \times \text{width of strip} = f(x)\ dx$.

Your job is to figure out a formula for $f(x)$.

But first you need to settle on a coordinate system. So pick one. If it were me, I would shift to a coordinate system with the center of the square as the origin. But you can make whatever choice you would like.

Yes I'm trying to use the negative mass trick

OK, we can do that once you have the mass and center of gravity of the triangle.

 

[Chestermiller]

So you decided not to consider the hint I gave you in post #3?

 

[Steve4Physics]

... So as we expected for a homgeneous square, the center of mass is in the middle.
Therefore, xc = yc = 7.5.

There is no need to use calculus to find the CoM of a uniform square. You can simply say that, from symmetry, its CoM is at its centre.

It might be worth noting that if you are allowed to use the standard result for the position of a triangle's CoM, the entire problem can be solved (e.g. using @Chestermiller's Post #3 hint) in about 3 lines of simple (non-calculus) working.

 

[JohnnyLaws]

So you decided not to consider the hint I gave you in post #3?

I don't understand How can I get the solution by calculating moment. How can I calculate a moment applied in this figure?

 

[JohnnyLaws]

Pick a coordinate system and use it. It seems that you have used the lower left corner of the square as your origin so far. You could continue to use that. That would be handy since your computed center of mass for the triangle would be in the same coordinate system you used for the square.

Or you could shift to a different coordinate system. For instance, one with its origin at the left hand corner of the triangle (which is also the center of the square). That would likely make the horizontal integral easier to evaluate. But it would mean that your triangle center of mass would be in a different coordinate system from your square's center of mass.

Either choice will work.OK, that sounds right.The $y$ coordinate is irrelevant when evaluating the horizontal center of mass. It would be relevant when evaluating the vertical center of mass. But an argument from symmetry immediately reveals where the vertical center must be.Remember that the incremental area is a strip that is $dx$ in width. Its height is enough to go from the top of the triangle (at the position of the strip) to the bottom. If you had a formula for that top to bottom height, you could compute $dA = \text{height at position x} \times \text{width of strip} = f(x)\ dx$.

Your job is to figure out a formula for $f(x)$.

But first you need to settle on a coordinate system. So pick one. If it were me, I would shift to a coordinate system with the center of the square as the origin. But you can make whatever choice you would like.OK, we can do that once you have the mass and center of gravity of the triangle.

I already understood the exercise. Thanks for your help!

 

[haruspex]

I don't understand How can I get the solution by calculating moment. How can I calculate a moment applied in this figure?

The moment of the weight of a body about an axis is the weight multiplied by the horizontal distance from the axis to the mass centre.
You can use that to find the moments of the complete square and the triangle, add (subtract) those to get the moment of the given shape, then use it again to find the distance to the mass centre.