Centripetal/Centrifugal Motion on a merry-go-round

[AAAA]

Homework Statement

You are standing 2.7 m from the centre of a spinning merry-go-round holding one end of a string tied to a 120g mass. The merry-go-round has a period of 3.9 s.

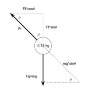
• Draw a system diagram of the situation.
• Draw an FBD of the mass in Earth's frame of reference.
• Draw an FBD of the mass in the merry-go-round's rotating frame of reference.
• What angle does the string make with the vertical?
• Determine the magnitude of the tension in the string.

My issue arises with the final question only (which is at the end of this admittedly long post), however, I would appreciate it if you folks could look over my FBDs as well, the rest is only ancillary.

Homework Equations

• Fac = (mv^2)/r
• V = d/t
• circumference = pi * diameter
• Fg = mg

3. The Attempt at a Solution
A.
I drew a person on the outside of the merry-go-round, and the string he holds follows a path some amount below the horizontal where it connects to the 120g mass. Like this:

----------------------------------------------------------------------------------------

B.

----------------------------------------------------------------------------------------

C.

----------------------------------------------------------------------------------------

D: (My solution matches the textbook's)

FNET_Y

1. Fnet_Y = Fg - Ft sin x = 0
2. Ft sin x = Fg
3. Ft = mg / sin x

FNET_X

1. mv^2/r = Ft cos x
2. mv^2/r = (mg/sin x) * cos x
3. V^2 = g/sin x * cosx
4. rearrange for x
5. rg/v^2 = tan x

SOLVE FOR VELOCITY

1. v = d/t
2. v = circumference / 3.9s
3. v = 2 * pi * r / 3.9s
4. v = ~4.34m/s

SOLVE FOR THETA

1. tan-1(rg/v^2)
2. tanx-1[(2.7*9.8)/4.34m/s^2]
3. x = 54 degrees
4. since they're asking for the angle from the vertical, it would be the complementary to this one
5. 90- ~54 = 36degrees

----------------------------------------------------------------------------------------

E:

1. Using one of my previous equations to solve for Ft
2. Ft = mg/sinx
3. Ft = 9.8*0.12/sin(54)
4. Ft = 1.45N

The bold is what I get wrong, the textbook's solution reads 0.96N, which would not even be equivalent to the Fg which (I presumed) the string counter-acted.

Where did I go wrong in my solution?

EDIT: The textbook's solution is wrong. I found the solution manual and they did the following operations

1. cos x = Fg / Ft (x being the angle from the vertical)
2. Ft = cosx * Fg

They should have obviously had Fg/cosx as Ft.

Ah well, good learning experience

 

[TSny]

Good work on getting the tension. Your free body diagram for (b) looks good, although I don't understand the "[toward center]" label. For the diagram in (c), why did you change the direction of the tension force. Also, in (c) there should be a third force in the diagram representing the centrifugal force.

 

[AAAA]

Good work on getting the tension. Your free body diagram for (b) looks good, although I don't understand the "[toward center]" label. For the diagram in (c), why did you change the direction of the tension force. Also, in (c) there should be a third force in the diagram representing the centrifugal force.

The towards center is actually incorrect, now that I look at it again. Thanks for catching my mistake! The acceleration towards the center is a component of the Ft, not Ft itself.

My intent with the changing of direction was that from the frame of reference of the merry-go-round, the tension was pulling it outwards.

But what it should be is the following, no?

My issue with this is that wouldn't that mean that Fc balances the x-component Ft?

Which perhaps makes sense because the object is technically moving at a constant velocity tangential to the circle, correct?

 

[TSny]

The string should point in the same direction in both diagrams; that is, up and to the left if the central axis of the merry-go-round is to the left. Therefore, F_T should point in the same direction in both diagrams. In the frame of the merry-go-round, the 120 g mass is at rest. So, the three forces F_T, mg, and F_centrifugal add to zero.

 

[AAAA]

The string should point in the same direction in both diagrams; that is, up and to the left if the central axis of the merry-go-round is to the left. Therefore, F_T should point in the same direction in both diagrams. In the frame of the merry-go-round, the 120 g mass is at rest. So, the three forces F_T, mg, and F_centrifugal add to zero.

Right! Makes sense, thanks again!

 

[skye2018]

**I've updated the diagram, hope this is a bit clearer

The textbook's answer is actually correct for d) & e)

d)

Horizontal component
Fnet=Ft*cos*theta
m*ac=Ft*cos*theta
Ft= (m*ac)/(cos*theta)

Vertical component
Fnet=m*g-Ft*sin*theta=0
m*g=Ft*sin*theta
**sub in Ft= (m*ac)/(cos*theta)**
m*g=[(m*ac)/(cos*theta)]*sin*theta
m*g=(m*ac)(tan*theta)
**m will cancel out**
g=(ac)(tan*theta)
theta=tan^-1(g/ac)
**ac=(4Pi^2*r)/(T^2)**
theta=tan^-1[g/(4Pi^2*r)/(T^2)]
theta=54.46 degrees

you're looking for Beta, so :
beta= 90-54.46
beta=~36 degrees

e)

Ft= mg*sin*theta
Ft=(0.12kg)(9.81)sin(54.46)
Ft=~0.96 N

 

[haruspex]

Ft= mg*sin*theta

No. In the direction of the string, you also have a component of centrifugal force (or, equivalently, there is a component of centripetal acceleration in that direction).
In your diagram you had, correctly, the vertical force F_tsin(θ) balancing mg, so the equation is mg=F_tsin(θ).

 

[skye2018]

No. In the direction of the string, you also have a component of centrifugal force (or, equivalently, there is a component of centripetal acceleration in that direction).
In your diagram you had, correctly, the vertical force F_tsin(θ) balancing mg, so the equation is mg=F_tsin(θ).

I'm not quite sure what you are meaning to say. Ft does equal mg*sin*theta in magnitude, and yes mg is equal to Ft*sin*theta in magnitude. **Note that mg and Ft are not on the same plane, so m*g=Ft*sin*theta cannot be rearranged to solve for Ft. Rearranging that would give you the incorrect answer of 1.45N. Centripetal force is defined as, “The component of force acting on a body in curvilinear motion that is directed toward the center of curvature or axis of rotation,” while centrifugal force is defined as, “The apparent force, equal and opposite to the centripetal force, drawing a rotating body away from the center of rotation, caused by the inertia of the body,” Which in my diagram centrifugal force would be mg*sin*theta, which is then equal in magnitude to the force of tension (centripetal force).

In summary, Ft= mg*sin*theta

https://www.livescience.com/52488-centrifugal-centripetal-forces.html

**Note, more reading on Centripetal force and acceleration: http://theory.uwinnipeg.ca/physics/circ/node6.html

 

[skye2018]

I'm not quite sure what you are meaning to say. Ft does equal mg*sin*theta in magnitude, and yes mg is equal to Ft*sin*theta in magnitude. **Note that mg and Ft are not on the same plane, so m*g=Ft*sin*theta cannot be rearranged to solve for Ft. Rearranging that would give you the incorrect answer of 1.45N. Centripetal force is defined as, “The component of force acting on a body in curvilinear motion that is directed toward the center of curvature or axis of rotation,” while centrifugal force is defined as, “The apparent force, equal and opposite to the centripetal force, drawing a rotating body away from the center of rotation, caused by the inertia of the body,” Which in my diagram centrifugal force would be mg*sin*theta, which is then equal in magnitude to the force of tension (centripetal force).

In summary, Ft= mg*sin*theta

https://www.livescience.com/52488-centrifugal-centripetal-forces.html

**Note, more reading on Centripetal force and acceleration: http://theory.uwinnipeg.ca/physics/circ/node6.html

Nevertheless if I am wrong, I'm no genius computer after all, I am simply a teenager and I have happened to have done it the way the textbook has done it. If there is flaws please do correct me.

 

[skye2018]

View attachment 222220
**I've updated the diagram, hope this is a bit clearer

The textbook's answer is actually correct for d) & e)

d)

Horizontal component
Fnet=Ft*cos*theta
m*ac=Ft*cos*theta
Ft= (m*ac)/(cos*theta)

Vertical component
Fnet=m*g-Ft*sin*theta=0
m*g=Ft*sin*theta
**sub in Ft= (m*ac)/(cos*theta)**
m*g=[(m*ac)/(cos*theta)]*sin*theta
m*g=(m*ac)(tan*theta)
**m will cancel out**
g=(ac)(tan*theta)
theta=tan^-1(g/ac)
**ac=(4Pi^2*r)/(T^2)**
theta=tan^-1[g/(4Pi^2*r)/(T^2)]
theta=54.46 degrees

you're looking for Beta, so :
beta= 90-54.46
beta=~36 degrees

e)

Ft= mg*sin*theta
Ft=(0.12kg)(9.81)sin(54.46)
Ft=~0.96 N

**could have directly found Beta, but this causes us to find the inverse of COT, and unfortunately my calculator doesn't have that function.

 

[haruspex]

Ft does equal mg*sin*theta in magnitude, and yes mg is equal to Ft*sin*theta in magnitude

They cannot both be true. It should be evident that Ft>mg.

Note that mg and Ft are not on the same plane, so m*g=Ft*sin*theta cannot be rearranged to solve for Ft.

Nonsense. As vectors they are not in the same direction, but including a sin() factor does not solve that. The vectors would still be in different directions, so not equal. The only way that equation can make sense is in regard to magnitudes.

As I posted, the flaw with Ft = mg*sin*theta is that you are ignoring centrifugal force. That has a component in the direction of the string. The correct equation would be Ft = mg*sin(θ)+(mv²/r)cos(θ).