- #1
Beth N
- 41
- 4
Homework Statement
Problem 6.7[/B]
Radius of curve: 200m
Speed: 90 km/h=90000m/h
What should be the value of the banking angle if no dependence is to be placed on friction?
Homework Equations
##F=ma##
##F_c=\frac {mv^2} {r}##
##w=mg##
Trig functions
The Attempt at a Solution
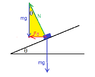
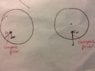
I got an answer that is flipped from the book’s key. My work is below:N=normal force
##N=F_c * sin \theta = \frac {mv^2} {r}* sin \theta ##
##N=w*cos \theta=mg*cos\theta##
##\frac {mv^2} {r}* sin \theta = mg*cos\theta##
##\frac {sin \theta} {cos\theta} =tan \theta= \frac {gr} {v^2}##
However, the key says that ##tan\theta= \frac {v^2} {gr}## For example I’m particularly not sure how they set up the equation ##w= N cos \theta## .I thought it should be ## N= w cos\theta##? I tried to draw out the triangle diagram but still can't figure it out.
Thank you!