Finding slip-off angle for mass off of sphere?

[giraffe714]

Homework Statement

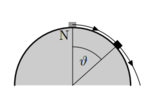
A point mass is placed at the north pole of a ball within a homogeneous vertical gravitational field with acceleration g. The mass therefore resides in an unstable equilibrium
from which it is removed by a negligibly small kick. It then glides without friction down
the surface of the ball. At which angle θ does the mass lift off from the surface of the
ball? Hint: To obtain the velocity of the mass as a function of the angle, you can use conservation
of energy. Alternatively, you can multiply the equation of motion for θ(t) by $\dot{\theta}$ and
integrate over time.

Relevant Equations

$\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta}} = \frac{\partial L}{\partial \theta}$, L = T - V

[Rewriting this as per the suggestions. Thanks once again.]

I won't be using the Lagrangian because it was never explicitly stated that I have to so I'll just use conservation of energy.

$$ T = \frac{1}{2}mv^2 = \frac{1}{2}m(R\dot{\theta})^2 = \frac{1}{2}mR^2\dot{\theta}^2 $$
$$ V = mgy = mgRcos\theta $$

At the topmost point, just when the mass is being pushed, the kinetic energy is 0 because the velocity is 0. At the topmost point since $\theta$ is 0 $cos\theta$ = 1, therefore $V = mgR$

Since T + V is constant, we can write this as

$$ \frac{1}{2}mR^2\dot{\theta}^2 + mgRcos\theta = mgR $$

The units of the kinetic energy are kg*m^2*rad^2/s^2, but since radians aren't technically units this just becomes kg*m^2/s^2 or J. $mgRcos\theta$ also holds up, kg*m/s^2*m or once again J. Same thing with the right hand side.

Now we can cancel out m's and R's:

$$ \frac{1}{2}R\dot{\theta}^2 + gcos\theta = g $$

Which then gives that

$$ \frac{1}{2}R\dot{\theta}^2 = g - gcos\theta \rightarrow \dot{\theta}^2 = \frac{2g - 2gcos\theta}{R} \rightarrow \dot{\theta} = \sqrt{\frac{2g - 2gcos\theta}{R}} $$

Is this dimensionally consistent? On the left side we have rad/s (or just 1/s), and on the right side we have... $\sqrt{\frac{m/s^2}{m}} = \sqrt{1/s^2} = 1/s$ Yes, that checks out so far.

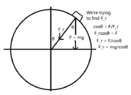
Now for the constraint condition: F_r = F_c. $F_r = mg/cos\theta$ (once again from diagram) and $F_c = \frac{mv^2}{R}$, the latter of which is also from my textbook so I would really hope it's dimensionally consistent . Also, $v = R\dot{\theta}$.

$$ \frac{mg}{cos\theta} = \frac{mv^2}{R} \rightarrow \frac{mg}{cos\theta} = \frac{mR^2\dot{\theta}^2}{R} = mR\dot{\theta}^2 \rightarrow \frac{g}{cos\theta} = R\dot{\theta}^2 $$

This is certainly cleaner than whatever I wrote down last time so I'm hoping this actually works out. As for the units, the left side has units of m/s^2 and the right has units of 1/s^2*m. I'm just ignoring the radians because they're dimensionless units and don't affect this analysis.

$$ \frac{g}{cos\theta} = R\frac{2g - 2gcos\theta}{R} \rightarrow cos\theta = 2 - 2cos\theta $$

$$ 1 = \frac{2}{cos\theta} - 2 \rightarrow 3 = \frac{2}{cos\theta} \rightarrow cos\theta = \frac{2}{3} $$

$$ \theta = arccos\frac{2}{3} $$

And even the units check out, so, I guess I solved it? If there are still any errors do point them out but I actually think I did get everything this time. Thanks for the help folks!

 

[PeroK]

I haven't checked your work, but $\dfrac {R^3}{g}$ is dimensionally inconsistent as an answer.

 

[PeroK]

PS I'm not sure why you needed the Lagrangian. Why not conservation of energy?

 

[giraffe714]

PS I'm not sure why you needed the Lagrangian. Why not conservation of energy?

The problemset was on the Lagrangian, I guess I just didn't realise there was an easier way. Thanks for pointing it out though.

 

[kuruman]

You have not specified the generalized coordinates in a diagram. In my opinion, that is a must when you use Lagrangians. Furthermore, you have been rather cavalier with the constraint that the mass stay on the sphere. This is how I would do it.
Define Cartesian coordinates $x$ and $y$ with the origin at the center of the sphere. Then
$T=\frac{1}{2}m\left(\dot x^2+\dot y^2\right)$
The constraints are $x=R\sin\theta~\implies \dot x=R~\dot {\theta}\cos\theta$
$y=R\cos\theta~\implies \dot y=-R~\dot {\theta}\sin\theta$
Therefore
$T=\frac{1}{2}m\left(R^2~\dot {\theta}^2\cos^2\theta+R^2~\dot {\theta}^2\sin^2\theta\right)=\frac{1}{2}mR^2~\dot {\theta}^2.$

Furthermore, what is this?
$\frac{\partial L}{\partial \theta} = -mg\dot{\theta}*-sin\theta = mg\dot{\theta}sin\theta$
The only explicit dependence of the Lagrangian on $\theta$ is in the potential term. The partial derivative of $\dot {\theta}$ with respect to $\theta$ is zero.

 

[giraffe714]

You have not specified the generalized coordinates in a diagram. In my opinion, that is a must when you use Lagrangians. Furthermore, you have been rather cavalier with the constraint that the mass stay on the sphere. This is how I would do it.
Define Cartesian coordinates $x$ and $y$ with the origin at the center of the sphere. Then
$T=\frac{1}{2}m\left(\dot x^2+\dot y^2\right)$
The constraints are $x=R\sin\theta~\implies \dot x=R~\dot {\theta}\cos\theta$
$y=R\cos\theta~\implies \dot y=-R~\dot {\theta}\sin\theta$
Therefore
$T=\frac{1}{2}m\left(R^2~\dot {\theta}^2\cos^2\theta+R^2~\dot {\theta}^2\sin^2\theta\right)=\frac{1}{2}mR^2~\dot {\theta}^2.$

Furthermore, what is this?
$\frac{\partial L}{\partial \theta} = -mg\dot{\theta}*-sin\theta = mg\dot{\theta}sin\theta$
The only explicit dependence of the Lagrangian on $\theta$ is in the potential term. The partial derivative of $\dot {\theta}$ with respect to $\theta$ is zero.

If I'm understanding this correctly, the constraints represent the angle $\theta$ when the mass slips off, correct? Or are you simply rewriting everything in Cartesian coordinates?

As to answer your question of "what is this," it is my attempt at applying the chain rule in a place where it should not have been applied. I will modify that right away, thanks for pointing it out.

 

[PeroK]

If I'm understanding this correctly, the constraints represent the angle $\theta$ when the mass slips off, correct? Or are you simply rewriting everything in Cartesian coordinates?

As to answer your question of "what is this," it is my attempt at applying the chain rule in a place where it should not have been applied. I will modify that right away, thanks for pointing it out.

I've looked at your original post and it has many errors. It needs a complete rewrite - including checking for dimensional coinsistency at every step.

As the equation of motion can be found from conservation of energy, you should do this and use it to confirm that your Lagrangian derivation is correct.

 

[kuruman]

f I'm understanding this correctly, the constraints represent the angle θ when the mass slips off, correct?

Incorrect. It is a generalized coordinate (as shown in the picture that you posted) that replaces $x$ and $y$ subject to the constraint that the mass stay on the sphere. The angle at which the mass slips off is a specific value of $\theta$ that you are asked to find. After you rewrite the Lagrangian in terms of $\theta$ and $\dot{\theta}$, you get the equation of motion from $$\frac{d}{dt}\left(\frac{\partial \mathcal L}{\partial \dot {\theta}}\right)-\frac{\partial \mathcal L}{\partial {\theta}}=0.$$I strongly second @PeroK 's suggestion

As the equation of motion can be found from conservation of energy, you should do this and use it to confirm that your Lagrangian derivation is correct.