Challenge V: Sylvester-Gallai Theorem, solved by Mandelbroth

[micromass]

Let's put up a new challenge:

This is called the Fano plane:

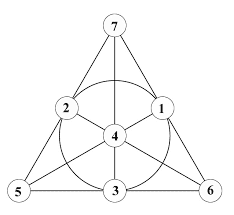
This is a geometric figure consisting of 7 points and 7 lines. However, it is a so-called projective plane. This means that it satisfies the following axioms:
1) Through any two points, there is exactly one line
2) Any two lines meet in exactly one point
3) There are four point such that no line goes to more than two of them

The study of projective planes and spaces goes deep and far. But for now, I'm asking something simpler. When you look at the figure, you see that one of the "lines" is actually a circle and not a straight line. Prove that you can't draw the above configuration on a plane such that all the lines are actually straight lines.

If you find this too easy, then there is this generalization:
Given $n$ points on a plane. If they do not all lie on a straight line, then there is a straight line in the plane that contains exactly two of the points.

 

[Mandelbroth]

If you find this too easy, then there is this generalization:
Given $n$ points on a plane. If they do not all lie on a straight line, then there is a straight line in the plane that contains exactly two of the points.

Suppose $n=1$.

 

[jostpuur]

Suppose $n=1$.

Then, out of the collection of points, in which there is only one point, all lie on a straight line (IMO) (on many straight lines to be more precise). The claim which is to be proven has the same form as $(0=1)\rightarrow \cdots$, and it will be true.

 

[micromass]

Suppose $n=0$.

Zero points still lie on one line. Indeed, given any line $L$, we have $\emptyset\subseteq L$.

 

[Mandelbroth]

Then, out of the collection of points, in which there is only one point, all lie on a straight line (IMO) (on many straight lines to be more precise). The claim which is to be proven has the same form as $(0=1)\rightarrow \cdots$, and it will be true.

Nevermind. I was correct in what I was saying. $n\in\{0,1\}$ is trivial (as is $n=2$).

I should stop second guessing myself.

 

[jostpuur]

Cases $n\in\{0,1,2,3\}$ proven. We are making progress.

I guess we are not in position of speaking about "generalization" of the challenge, since we haven't reached $n=7$ yet...

(edit: Actually I don't yet know what to do with the case n=7 either... looks tough..)

 

[Mandelbroth]

Cases $n\in\{0,1,2,3\}$ proven. We are making progress.

I might as well do $n>3$ as well.

Suppose, by way of contradiction, that there are $n$ points, not all of which are collinear but with at least 3 points on each line connecting any 2 points. Let $r$ be the smallest distance between a line $l$ and a point $x$ not on that line. Because $l$ goes through at least 3 of the $n$ points, for a segment $R$ of length $r$ from $x$ to $l$ there are two cases:

• The segment intersects $l$ at one of the $n$ points and there is exactly 1 point on either side of the segment, implying the rest of the points are contained in the line containing $R$, in which case there is a line between only one of the points on either side and $x$, reaching a contradiction.
• There are at least two points on one side of the line containing $R$. Call the point closer to the segment $a$, and a further point $b$. Let $m$ be the line that connects $x$ and $b$. The distance from $a$ to $m$ is less than $r$, reaching a contradiction.

Thus, $x$ must be on $l$ if every line connecting 2 points contains at least 3 of the $n$ points. The result follows.

 

[jostpuur]

... The distance from $a$ to $m$ is less than $r$, reaching a contradiction.

I believe I drew a picture of the situation you described, and I don't see a contradiction.

 

[Mandelbroth]

I believe I drew a picture of the situation you described, and I don't see a contradiction.

You believe you drew a picture or you believe there isn't a contradiction? :tongue:

I've attached my drawing. I can show all the trig if you want, but it's fairly clear that the distance from $a$ to $m$ is less than $r$.

 

[jostpuur]

I know I drew something.

What two claims are contradictory in "the contradiction"?

 

[Mandelbroth]

I know I drew something.

What two claims are contradictory in "the contradiction"?

For the second case, $r$ is taken to be the smallest distance between a line and a point not on that line, which I named $l$ and $x$ (respectively) for convenience. However, the distance from $a$ to $m$ is smaller than $r$ (implying that there isn't a smallest distance between a line and a point not on that line).

If all lines containing 2 of the $n$ points contain at least 3 of them, then they must all, therefore, be collinear.

 

[jostpuur]

ok, I had not understood your explanation properly. I guess I'll remove my picture now -->

 

[jostpuur]

Let $r$ be the smallest distance between a line $l$ and a point $x$ not on that line.

To clarify to other readers, this means that we go through all possible lines ell connecting some points, and for all fixed ell, again through all possible points x not on that ell. Then the final ell and x are chosen so that their distance is minimal.

This looks like a good start, but I didn't yet understand how the final steps of the proof were supposed to work.

Mandelbroth, can you clarify what you assume about the points a and b with respect to the line ell? Are completely free of it, or do you insist that one or both of them are on ell?

 

[Mandelbroth]

To clarify to other readers, this means that we go through all possible lines ell connecting some points, and for all fixed ell, again through all possible points x not on that ell. Then the final ell and x are chosen so that their distance is minimal.

This looks like a good start, but I didn't yet understand how the final steps of the proof were supposed to work.

Mandelbroth, can you clarify what you assume about the points a and b with respect to the line ell? Are completely free of it, or do you insist that one or both of them are on ell?

The existence of at least one of the points is guaranteed by the fact that each line contains at least three of the $n$ points in both cases. In the second case, $a$ and $b$ are shown to exist because of this definition, and I did the trig calculations for the distance from $a$ to $m$ that way. In general, I suppose they are not required to be on $l$, though. My proof uses the fact that there is a pair $a$ and $b$ that must exist under the assumptions of the proof.

For the final part of the proof, if $r$ cannot exist with the beginning conditions, then there isn't a smallest distance between a line and a point not on that line under those conditions. We thus conclude that the points must all be on the same line.

Edit: misunderstanding the confusion. See below.

 

[jostpuur]

This:

Mandelbroth, can you clarify what you assume about the points a and b with respect to the line ell? Are completely free of it, or do you insist that one or both of them are on ell?

Clarify!

In your drawing the a and b are not on ell, right? In that case your claim doesn't seem valid. It is possible that the distance between m and a is greater than r too.

Your claim conserning the distance seems correct if a and b are on ell, but then we have other problems with the logic of the proof attempt.

 

[Mandelbroth]

This:



Clarify!

In your drawing the a and b are not on ell, right? In that case your claim doesn't seem valid. It is possible that the distance between m and a is greater than r too.

I did!
I apologize. That would explain the confusion. I should fix that.

Your claim concerning the distance seems correct if a and b are on ell, but then we have other problems with the logic of the proof attempt.

Why?

 

[jostpuur]

This can happen:

 

[Mandelbroth]

This can happen:

Indeed, but a pair $a$ and $b$ satisfying the results of the proof are given to exist on the line.

I'm asking about the logic of the proof attempt.

 

[verty]

Proving that generalization by strong induction definitely seems possible, although there is a hurdle to overcome. I won't prove it though, I'll leave it to anyone else who would like to try it.

 

[jostpuur]

I'm asking about the logic of the proof attempt.

In the original proof attempt you divided the proof into two possible situations. In the same spirit I do a similar division now:

Situation 1: When the line R splits the line ell into two pieces, both sides contain precisely one point on ell. (According to our anti-thesis, the line ell also must contain a third point at the intersection of ell and R.)

Situation 2: When the line R splits the line ell into two pieces, at least other side contains at least two points on ell.

I haven't checked any trigonometry yet, but it seems that in situation 2 we arrive at a contradiction as you showed in the second attachment drawing. So that half is ok.

The first situation becomes a mystery. I don't see how we get a contradiction there.

In the original proof attempt you made the following claim:

Assume that when the line R splits line ell into two pieces, both sides contain precisely one point on ell, and also assume that no other points exist outside the line R. Then a contradiction follows.

This claim was correct, but there are too much assumptions for the complete proof.

 

[jostpuur]

This can happen too:



Now ell and x don't seem very useful when searching for the line that contains only two points.

update: But now looking at the picture, I can see that actually that cannot happen. It has a contradiction hidden in it...

 

[Mandelbroth]

This can happen too:



Now ell and x don't seem very useful when searching for the line that contains only two points.

update: But now looking at the picture, I can see that actually that cannot happen. It has a contradiction hidden in it...

I just realized why you and micro were so confused by my case 1. :yuck:

However, we can fix that by simply making the point of intersection be $a$, in which case it works the same as the second case.

 

[jostpuur]

Given $n$ points on a plane. If they do not all lie on a straight line, then there is a straight line in the plane that contains exactly two of the points.

IMO this has now been proven. Only nuisance left to readers is that the proof is not written clearly in one place, but its pieces are scattered among confusing discussion... But the necessary pieces have been checked.

The special problem with n=7 remains unsolved, despite the solved problem being a "generalization".

 

[jostpuur]

So do you see why, in case 1, there must be only one point on either side of the line containing segment $R$, with the rest collinear within that line, or should I explain further?

Contradiction implies anything, but notice, that even if there were only one point on each side of the line R, a contradiction would still be present...

 

[Mandelbroth]

Contradiction implies anything, but notice, that even if there were only one point on each side of the line R, a contradiction would still be present...

See the above. I edited my post when I reread my proof. The solution should be clearer now.

 

[Theorem.]

I just completed a proof using contradiction and the smallest positive distance between point line pairs. I'll post it after I am off work (which won't be for 8 hours): )

 

[micromass]

So, this challenge was solved by Mandelbroth, after some refining with the help of jostpuur. Nice done guys!

I would be interested to see Theorem.'s approach.

A full discussion of this theorem and proof can be found on wiki: http://en.wikipedia.org/wiki/Sylvester–Gallai_theorem The proof given here is essentially Kelly's proof, which is known as one of the most elegant proofs in mathematics.

Our proof required both an ordering (we wanted to say that a point is between two other points), and a metric (we wanted to talk about distances). It is interesting to know that there is a proof that only requires an ordering!

I'll post the new challenge soon!

 

[jostpuur]

true co-operative research!

 

[Theorem.]

Well it looks like my proof is a slightly more detailed (and I admit less elegant) version of Kelly's proof. I can still post it if anyone is still interested though!

 

[micromass]

Well it looks like my proof is a slightly more detailed (and I admit less elegant) version of Kelly's proof. I can still post it if anyone is still interested though!

Sure, post it!

 

[Theorem.]

Sure, post it!

$\textbf{Definition}[\text{set of lines generated by a set of points in the plane}]: \\ \text{ Given any two points on the plane }p_1,p_2\text{, let } L_{p_1 p_2} \text{ denote the line going through the two points.}\\ \text{We will call this the line generated by }p_1 \text{ and }p_2.$

$\text{If } P \text{ is a finite set of points in the plane, Let } L_P:=\{L_{p_i p_j}: p_i,p_i\in P, i\neq j\}. \\ \text{ We will call this the set of lines generated by P}$


Okay, now we can focus a bit on the question!. We want to show that given any finite set of points
$P$ in the $\mathbb{R}^2$, if not all the points lay on a straight line, then there exists a line going through exactly two of the points. We will do this by contradiction. As I mentioned before, This is basically Kelly's proof (Which Micromass mentioned earlier), I may have seen it on a problem set earlier on, but the idea struck me regardless. Let us begin.

Suppose towards a contradiction there exists a finite set of points
$P=\{p_1,p_2,...,p_n\}\subset \mathbb{R}^2$ with the property that $|L\cap P|\geq 3$ for all $L\in L_P$. That is, every line in $L_P$ intersects at least
3 points of $P$.

Consider the set $D:=\{d(p,L): p\in P, L\in L_P \thinspace and \thinspace p\notin L\}$. This set is finite and bounded below by 0, and thus has a minimum $a>0$. Let $p,L$ be such that $d(p,L)=a$.

It is intutively helpful after this point to visualize what is going on graphically (on paper).

Connect $p$ to $L$ by forming the line perpendicular to $L$ that goes through $p$, We can call this line $PL$, and notice that it must have length $a$. By the initial assumption, the line $L$ intersects at least 3 points of $P$, so at least two of these points must lay to one side of the point where $L$ and $PL$ intersect (as Kelly's proof points out- it is of course okay for one of these points to be exactly on the intersection). Denote the point closest to the intersection $q_1$ and the point furthest $q_2$. Then $L_{q_2 p}\in L_P$. Form
The line $L_2Q$ perpendicular to $L_{q_2 p}$ and through $q_1$. Then it is easy to see that $d(q_1,L_{q_2 p})<d(p,L)$. As Kelly's proof suggests, you can just note that the triangle with hypotenuse $q_1q_2$ is similar to the triangle with hypotenuse $pq_2$.

This of course contradicts the fact that $d(p,L)=\min{D}$, and we are done.

The proof is identical to Kelly's proof except the notation I used is definitely harsher and some small parts are explained differently. Minor differences that helped me work through the problem but at the end of the day can be cleaned up. I originally tried doing it by strong induction and got stuck for awhile but eventually got the right kind of idea! fun problem

 

[verty]

Darn, the idea I had for proving the generalization didn't work, the hurdle was more like an infinite slope. Instead one must use the number of lines; there are too many lines for all of them to have 3 points on. Each new point generates tons of new lines.

Anyway, I'm leaving this.