How to understand this 3d surface of ##P,\bar{V}##, and ##T##?

[zenterix]

TL;DR Summary

There is a surface shown in the book "Physical Chemistry" by Silbey, Alberty, and Bawendy that I would like to understand better.

Here is the figure I would like to understand

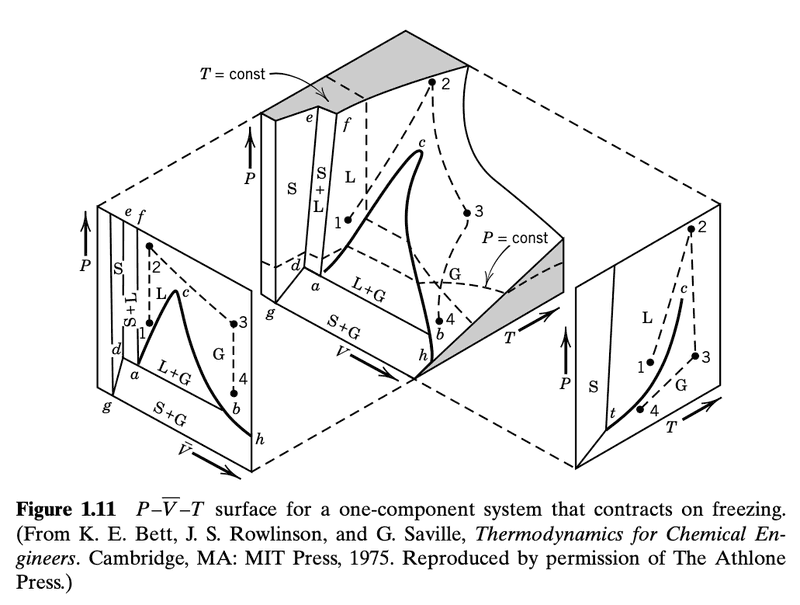
First of all, I don't see a specific surface. In the middle plot, I see what looks like the innards of a solid cube that has a large piece cut off.

There is also an arrow annotated as "T=const". It is not clear what this arrow is pointing to. I though it was the shaded plane but that doesn't seem correct. So, perhaps that small line segment on the shaded plane?

Furthermore, the book says that

"the state of a pure substance is represented by a point in a Cartesian coordinate system with $P, \bar{V}$, and $T$ plotted along the three axes. Each point on the surface of the 3D model in Fig. 1.11 described the state of a one-component system that contracts on freezing".

and that

"Projections of this surface on the $P-\bar{V}$ and $P-T$ planes are shown. There are three two-phase regions on the surface: S+G, L+G, and S+L. There three surfaces intersect at the triple point $t$ where vapor, liquid, and solid are in equilibrium".

The projection of the three-dimensional surface on the P –T plane is shown to the right of the main diagram in Fig. 1.11. The vapor pressure curve goes from the triple point t to the critical point c (see Section 1.7). The sublimation pressure curve goes from the triple point t to absolute zero. The melting curve rises from the triple point. Most substances contract on freezing, and for them the slope dP/dT for the melting line is positive.

Why is the slope dP/dT positive when substances contract on freezing?

Also, consider the following quote

"For a pure substance there is a critical point $(P_c , T_c)$ at the end of the liquid–gas coexistence curve where the properties of the gas and liquid phases become so nearly alike that they can no longer be distinguished as separate phases. Thus, $T_c$ is the highest temperature at which condensation of a gas is possible, and $P_c$ is the highest pressure at which a liquid will boil when heated."

In figure 1.11, I guess this is denoted as just $c$. I suppose that $P_c$ and $T_c$ are different for each volume and so for each $P_c$ and $T_c$ we have an associated $V_c$.

 

[Philip Koeck]

TL;DR Summary: There is a surface shown in the book "Physical Chemistry" by Silbey, Alberty, and Bawendy that I would like to understand better.

Here is the figure I would like to understand

View attachment 330596

First of all, I don't see a specific surface. In the middle plot, I see what looks like the innards of a solid cube that has a large piece cut off.

There is also an arrow annotated as "T=const". It is not clear what this arrow is pointing to. I though it was the shaded plane but that doesn't seem correct. So, perhaps that small line segment on the shaded plane?

Furthermore, the book says that
and that

Why is the slope dP/dT positive when substances contract on freezing?

Also, consider the following quote
In figure 1.11, I guess this is denoted as just $c$. I suppose that $P_c$ and $T_c$ are different for each volume and so for each $P_c$ and $T_c$ we have an associated $V_c$.

It's a "regular" substance meaning it's not like water. For water the slope of the surface showing equilibrium between solid and liquid (rectangle marked S+L) would be negative.
In this diagram you see that increasing P at constant T will change the substance from liquid to solid. For water the opposite happens.

You can look at individual slices through this diagram and you'll get the usual pV and pT diagrams (and VT if you want).
For example a slice at a constant and high value of T gives the pV diagram of an almost ideal gas.

Then you can also look at projections as shown in the figure. For example if you project along V you get the PT phase diagram. This is valid for a closed system where V is allowed to adapt freely.

In 3D the diagram shows what phase(s) the substance will have for given values of V, P and T for 1 mol (for example) of the substance.
Only values of V, P and T that lie on the shown surface are possible in a closed system though.

Actually the diagram requires more thinking than I realized.
Are things getting clearer?

And T = constant is any plane orthogonal to the T-axis. The arrow is plain confusion.

 

[zenterix]

Because we have a state equation of an ideal gas, we can't be at just any $P,\bar{V},$ and $T$. That is, we can only be at points that satisfy $P\bar{V}=RT$. This is a surface in 3d.

In the 3d diagram, what is the surface exactly? Is the white part a surface? Why are some lines solid and some lines dashed in the 3d figure?

Honestly, I don't think think I've ever seen a plot that I could understand less than this one. The issue is mainly the depiction, not the underlying concepts.

However, in terms of the concepts, I don't understand the two-phase regions very well either, maybe because it is so far from everyday experience.

Take S+G, for example. In the projection on the $P-\bar{V}$ plane (where temperature is fixed) we have a region with low pressure and increasing molar volume. In this region we have solid + gas phases. Does this mean that for any combination of pressure and molar volume in this region if we leave the system it will always have solid and gas phases? Like, solid pieces on the floor of the volume and gas filling up the space?

Then, consider the pink line on the left below

If we are in S+G and we increase the pressure then eventually we get to L+G and then to just G. Why does increasing pressure make a solid go to liquid and then to gas phase?

 

[zenterix]

Because we have a state equation of an ideal gas, we can't be at just any $P,\bar{V},$ and $T$. That is, we can only be at points that satisfy $P\bar{V}=RT$. This is a surface in 3d.

In the 3d diagram, what is the surface exactly? Is the white part a surface? Why are some lines solid and some lines dashed in the 3d figure?

Honestly, I don't think think I've ever seen a plot that I could understand less than this one. The issue is mainly the depiction, not the underlying concepts.

However, in terms of the concepts, I don't understand the two-phase regions very well either, maybe because it is so far from everyday experience.

Take S+G, for example. In the projection on the $P-\bar{V}$ plane (where temperature is fixed) we have a region with low pressure and increasing molar volume. In this region we have solid + gas phases. Does this mean that for any combination of pressure and molar volume in this region if we leave the system it will always have solid and gas phases? Like, solid pieces on the floor of the volume and gas filling up the space?

Then, consider the pink line on the left below

View attachment 330627

If we are in S+G and we increase the pressure then eventually we get to L+G and then to just G. Why does increasing pressure make a solid go to liquid and then to gas phase?

To answer the questions raised above:

When we move along the pink line, temperature is not constant. For each temperature, in the P-$\bar{V}$ plot we get some curve (an isothermal). If we change the temperature, we get another isothermal. Thus, in moving along the pink line we are moving to different isothermals. The only way to, e.g. increase pressure at constant $\var{V}$, is to increase the temperature.

Here is a simplified version of the projection on the $P-\bar{V}$ plane

To get from 1 to 2, we heat a liquid at constant volume. From 2 to 3, we move along an isothermal, meaning we keep the temperature constant and we expand the volume (which lowers the pressure). If we then cool the gas at constant volume we get to 4.

This particular path from 1 to 4 is how we get from a liquid to a gas "without the appearance of an interface between the two phases". Not sure what this means though. I can see that this path avoids the two-phase equilibrium points where we have L+G, but not sure what the cited "interface between the two phases" is.

The point c is called a critical point. At this point there is no distinction between gas and liquid.

 

[Philip Koeck]

Take S+G, for example. In the projection on the $P-\bar{V}$ plane (where temperature is fixed) we have a region with low pressure and increasing molar volume. In this region we have solid + gas phases. Does this mean that for any combination of pressure and molar volume in this region if we leave the system it will always have solid and gas phases? Like, solid pieces on the floor of the volume and gas filling up the space?

Just a quick remark here. For the projection onto pV temperature is not fixed but it adapts to whatever it has to be.
In the same way volume adapts in the pT projection (the usual phase diagram).

In the pT and the pV diagram the sustance can be anywhere, but in the 3D-diagram it can only be somewhere on the surface.

 

[Philip Koeck]

Here is a simplified version of the projection on the $P-\bar{V}$ plane

View attachment 330630

Here you clearly see that T is not fixed. It's different for every isotherm shown.

 

[Philip Koeck]

Then, consider the pink line on the left below

View attachment 330627

If we are in S+G and we increase the pressure then eventually we get to L+G and then to just G. Why does increasing pressure make a solid go to liquid and then to gas phase?

T has to increase such that the substance stays on the surface in 3D.
Here you see that T is not fixed in the pV projection.

 

[Philip Koeck]

To answer the questions raised above:

When we move along the pink line, temperature is not constant. For each temperature, in the P-$\bar{V}$ plot we get some curve (an isothermal). If we change the temperature, we get another isothermal. Thus, in moving along the pink line we are moving to different isothermals. The only way to, e.g. increase pressure at constant $\var{V}$, is to increase the temperature.

Here is a simplified version of the projection on the $P-\bar{V}$ plane

View attachment 330630

To get from 1 to 2, we heat a liquid at constant volume. From 2 to 3, we move along an isothermal, meaning we keep the temperature constant and we expand the volume (which lowers the pressure). If we then cool the gas at constant volume we get to 4.

This particular path from 1 to 4 is how we get from a liquid to a gas "without the appearance of an interface between the two phases". Not sure what this means though. I can see that this path avoids the two-phase equilibrium points where we have L+G, but not sure what the cited "interface between the two phases" is.

The point c is called a critical point. At this point there is no distinction between gas and liquid.

I think you're getting the hang of it. pVT diagrams provide you with hours of fun.

 

[zenterix]

fun=madness/pulling one's hair out?

 

[Philip Koeck]

Take S+G, for example. In the projection on the $P-\bar{V}$ plane (where temperature is fixed) we have a region with low pressure and increasing molar volume. In this region we have solid + gas phases. Does this mean that for any combination of pressure and molar volume in this region if we leave the system it will always have solid and gas phases? Like, solid pieces on the floor of the volume and gas filling up the space?

Somewhere you mention "interface between phases". That's just the lines in the projections for example in the PT phase diagram.

About 2 and 3-phase situations:
They can be realized in practice, but remember that the diagrams only talk about closed systems.
For example take the triple point in the PT diagram. This becomes a straight line parallel to the V-axis in the 3D diagram.
This simply means that if you have the substance at that pressure and temperature in a container with variable volume you will generally find all 3 phases, bits of solid in the liquid and gas above that.
You can vary the volume quite a lot and the only thing that changes is the ratio of the amounts.
If you make the volume very small you'll have only solid and if you make it very big you'll have only gas.

 

[TeethWhitener]

Here’s a video that just popped up in my YouTube feed where they explain PVT diagrams:

There are some good animations in here that make it a little clearer what’s going on.

 

[robphy]

https://skfb.ly/XCIA
https://sketchfab.com/3d-models/3d-phase-diagram-e4c0c142085749909de5dd93a8dd1636
is an interactive viewer (for 3d-printing)
that I found on
https://letsgeekblog.wordpress.com/2016/12/13/phase-diagrams-3d/

See also
https://sketchfab.com/3d-models/3d-phase-diagram-1c1b3730035943d9990dc6d157598b76
https://sketchfab.com/3d-models/p-v-t-phase-diagram-of-water-624b676076d04249a364d7651657ce18

https://biomodel.uah.es/Jmol/plots/phase-diagrams/inicio.htm