Change in reading of the scale when putting ball in a container of alcohol

[MatinSAR]

Homework Statement

We have a container in the shape of a cube whose side length is $10cm$. We pour alcohol with a density of $0.8g/cm^3$ up to a height of $8cm$. We put the container on the scale and the scale shows the number $700g$. We remove the container from the scale and put a solid ball with a density of $6g/cm^3$ in the container. Now we put the container on the scale again and the scale shows the number $2160g$. What is the mass of the bullet?

Relevant Equations

Newton's Laws.

The container and water inside it are at rest.

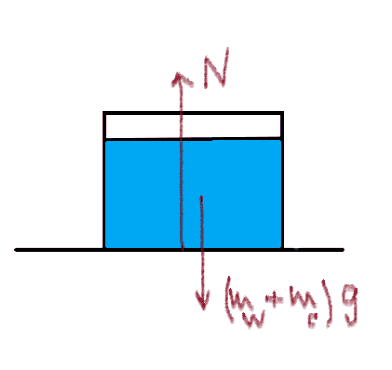
$F_{net,y}=ma_y$
$N - (m_{container}+m_{water})g = 0$
$N = (m_{container}+m_{water})g$
$m_{container}+m_{water}=700g$
$m_{container}+\rho_{water} V=700g$
$m_{container}+0.8(10*10*8)=700g$
$m_{container}=60g=0.06kg$

Now we put a ball in container so the number that scale show should change.
The volume of water displaced is equal to the volume of the ball. As a result, the water level should rise to a height of $0.08+ \dfrac {V_{ball}}{0.1*0.1}$.
$V_{ball}=\dfrac {m_{ball}}{ \rho_{ball}}$

We calculate new pressure:
$P=\rho g h_{new}=800*10* (0.08+ \dfrac {V_{ball}}{0.1*0.1})$

Now we calculate normal force sacle exerts on container:
$N = (m_{container}+m_{ball})g + PA$

But it gave me wrong answer. Can someone guide me where my mistake is?

​

 

[BvU]

So container + alcohol is 700 g
and container + alcohol + ball is 2160 g ?



$\$

 

[haruspex]

So container + alcohol is 700 g
and container + alcohol + ball is 2160 g ?



$\$

You are overlooking something.

 

[haruspex]

Can someone guide me where my mistake is?

​

@BvU's hint is a good start, but there's more to it. The next step is to calculate the volume of the ball that it implies.

 

[MatinSAR]

So container + alcohol is 700 g
and container + alcohol + ball is 2160 g ?



$\$

As question stated, yes.

@BvU's hint is a good start, but there's more to it. The next step is to calculate the volume of the ball that it implies.

The ball is completely in alcohol so we consider it's total volume.

 

[haruspex]

The ball is completely in alcohol so we consider it's total volume.

No, you are missing the point.
First, @BvU is hinting at a trivial calculation to find the mass of the ball. But having done that, the next step is to deduce its volume.

 

[kuruman]

No, you are missing the point.
First, @BvU is hinting at a trivial calculation to find the mass of the ball. But having done that, the next step is to deduce its volume.

Why is the volume needed? The question posed is "What is the mass of the bullet?"

On edit: I now see why the volume of the ball/bullet is needed.

 

[haruspex]

Why is the volume needed? The question posed is "What is the mass of the bullet?"

Bullet? Ball? Whatever. Unless it absorbs alcohol, the volume matters.

 

[erobz]

Bullet? Ball? Whatever. Unless it absorbs alcohol, the volume matters.

I confirm. They are being sneaky!

 

[nasu]

There is a reason they say that the container is not on the scale when they add the ball.

 

[MatinSAR]

There is no bullet. We have a ball in container. it was a mistake in my translation, sorry.

No, you are missing the point.
First, @BvU is hinting at a trivial calculation to find the mass of the ball. But having done that, the next step is to deduce its volume.

So it's mass should be 1460g.
$$V=\dfrac {m}{\rho}=\dfrac {1460}{6}=243.33cm^3$$

 

[erobz]

There is no bullet. We have a ball in container. it was a mistake in my translation, sorry.

So it's mass should be 1460g.
$$V=\dfrac {m}{\rho}=\dfrac {1460}{6}=243.33cm^3$$

Now do you notice something about the volume here?

 

[MatinSAR]

Now do you notice something about the volume here?

This way $43.33cm^3$ water should pour out of the container.

 

[haruspex]

This way $43.33cm^3$ should pour out of the container.

Right. So how are you going to find the mass of the ball? Try to write some equations, introducing new unknowns as necessary.

 

[erobz]

This way $43.33cm^3$ should pour out of the container.

Right, its over the volume remaining in the container. So you need to adjust your model to account for some mass of the alcohol spilling out of the container. Also, you don't have to look at pressures like you were before.

 

[MatinSAR]

Right. So how are you going to find the mass of the ball? Try to write some equations, introducing new unknowns as necessary.

Right, its over the volume remaining in the container. So you need to adjust your model to account for some mass of the alcohol spilling out of the container. Also, you don't have to look at pressures like you were before.

$$m_{container}+m_{alcohol}+m_{ball} = 1460g$$
$$60 + 0.8(800-43.33)+m_{ball} = 1460g$$
$$m_{ball} = 794.66g$$

 

[erobz]

$$m_{container}+m_{alcohol}+m{ball} = 1460g$$
$$60 + 0.8(800-243.33)+m{ball} = 1460g$$
$$m{ball} = 954.66g$$

It's an unknown amount of volume that spills out. You have to calculate it with a new model. Can't use the last one, because it didn't account for any spillage. You were acting as though it all stayed in the container on that one. When you found the volume of the ball is greater than what was left it invalidates the model you used to find its volume.

 

[MatinSAR]

It's an unknown amount of volume that spills out. You have to calculate it with a new model. Can't use the last one, because it didn't account for any spillage. You were acting as though it all stayed in the container on that one. When you found the volume of the ball is greater than what was left it invalidates the model you used to find its volume.

I was working on 2 questions at one time. I'm sorry for my huge mistake in last post. I will retry.

 

[MatinSAR]

$$m_{container}+m_{alcohol}+m_{ball}=2160$$$$60+0.8(1000-V_{ball})+6V_{ball}=2160$$$$V_{ball}=250cm^3$$$$m_{ball}=\rho_{ball} V_{ball}=1500g$$

Thank you to everyone who has helped me to solve this problem.