- #1
- 19,357
- 25,140
It's December and we like to do a Special this month. The challenges will be posted like an Advent Calendar. We will add a new problem each day, from 12/1 to 12/25. They vary between relatively easy logical and numerical problems, calculations, to little proofs which hopefully add some nice-to-know lemmata to your toolbox. We hope you will have fun with this format. In case open questions are too difficult and a new one isn't opened yet, we recommend https://www.physicsforums.com/threads/math-challenge-november-2018.960003/#post-6087946 where still some easy ones can be found.
Rules:
a) In order for a solution to count, a full derivation or proof must be given. Answers with no proof will be ignored. Solutions will be posted around 15th of the following month.
b) It is fine to use nontrivial results without proof as long as you cite them and as long as it is "common knowledge to all mathematicians". Whether the latter is satisfied will be decided on a case-by-case basis.
c) If you have seen the problem before and remember the solution, you cannot participate in the solution to that problem.
d) You are allowed to use google, wolframalpha or any other resource. However, you are not allowed to search the question directly. So if the question was to solve an integral, you are allowed to obtain numerical answers from software, you are allowed to search for useful integration techniques, but you cannot type in the integral in wolframalpha to see its solution.
Hints: on demand
1. (solved by @julian ) Let ##(a_n)_{n \in\mathbb{N}}\subseteq \mathbb{R}^+## be a sequence of positive real numbers and ##A=\sum_{n=1}^\infty a_n\,.## Prove the following statements:
Two mathematicians meet by chance on a plane: "Didn't you have three sons?" asks one, "how old are they?" - "The product of years is 36," is the answer, "and the sum of years is exactly today's date." "Hmm, that's not enough for me," says the colleague. "Oh, right," says the second mathematician, "I forgot to mention that my eldest son has a dog."
How old are the three sons?
All others are recommended to [/URL]https://www.physicsforums.com/threads/math-challenge-november-2018.960003/. Especially the problems 7,8,9,19,20 should be manageable, and even 15,16 look more complicated as they actually are. If you want a new problem despite of these:
2. b.) (solved by @jbstemp) The unitary matrices build a manifold, the Lie group ##SU(n)##. Calculate its tangent space at the neutral element of the group.
3. Find functions ##y(t)## and ##z(t)## which locally solve the equations
$$
\begin{cases}
e^t + \tan y(t) &= 1\\
t^2 + z(t)^3+z(t) &=0
\end{cases}
$$
in a neighborhood of ##t=0## and investigate their behavior with respect to monotony (where defined). It is sufficient to determine the functions up to a differential equation. It's a mathematical problem, so existence will do.
4. (solved by @DeathByKugelBlitz ) Find a ten digits integer with all ten digits, such that the first ##n## digits (##1\leq n \leq 10##) are divisible by ##n##. The integer should thus contain all ##10## different symbols ##0,1,2,3,4,5,6,7,8,9##.
5. Is there always a position on a floor (continuous, no holes, steps etc.) for a rectangular table with four equal legs, such that the table does not wiggle?
6. (solved by @SSequence ) Show that ##(0,1) \subset \mathbb{R}## cannot be written as a countable disjoint union of closed intervals.
7. Areas and Volumes
7.a.) (solved by @Delta2 ) Show that the paraboloid
$$P=\{\,(x,y,z)^\tau\in \mathbb{R}^3\,|\,x^2+y^2=z\, , \,x,y\in [-1,1]\,\} \subseteq \mathbb{R}^3$$
and the hyperboloid
$$H=\{\,(x,y,z)^\tau\in \mathbb{R}^3\,|\,x^2-y^2=z\, , \,x,y\in [-1,1]\,\} \subseteq \mathbb{R}^3$$
have equal areas.
7.b.) (unsloved) Bring ##M =\{\,(x,y,z)^\tau\in \mathbb{R}^3\,|\,x^2\leq y^4\leq z^8\leq 1\,\}## into a normal form and calculate its volume.
8. (solved by @Young physicist ) The table cards at a rotatable round table with 12 seats are set up for expected 12 guests. However, the persons ignore the cards and randomly distribute themselves to the seats.
Is it always possible with a single turn of the table to make sure that at least two people sit in front of their correct table cards?
9. Let ##p(x)=x^n+a_{n-1}x^{n-1}+\ldots +a_1x+a_0 \in \mathbb{R}[x]## be a polynomial where all roots are negative. Prove that $$\int_{1}^{\infty}\dfrac{1}{p(x)}\,dx$$ converges absolutely if and only if ##n>1\,.##
10. (solved by @Young physicist ) Tom bets John that he can do the following: John will recite ##99## different numbers in the range ##1 \ldots 100## (i.e. positive integers) in a random order and he will be able to find and name the only number in that range that John will have missed. Tom will do it without taking any notes. What is the best algorithmic strategy to use in order to accomplish this? Give the relevant math.
11. Let ##\emptyset \neq U \subseteq \mathbb{R}^+## be an open set, and ##x_0\in U\,.## We define the quotient logarithm of a function ##f\; : \;U \longrightarrow \mathbb{R}^+## at ##x=x_0## by
$$
f\,^-(x_0) := \lim_{x \to x_0} \dfrac{\log f(x)-\log f(x_0)}{\log x-\log x_0}
$$
Solve the 'differential equation' ##f^-=f\,.##
12. (solved by @lpetrich ) Let [itex]x_0=0,x_1=1[/itex], and [itex]x_{n+1}=n(x_n+x_{n-1})[/itex] for [itex]n\geq 1[/itex]. Find [itex]\lim_{n\to\infty}\dfrac{x_n}{n!} \quad[/itex].
13. (solved by @lpetrich ) Let ##p>q## be prime numbers such that ##p \not\equiv 1 \operatorname{mod}q##.
Prove that each group with ##pq## elements is cyclic.
14. (solved by @Young physicist ) If we multiply our five digits number by four, we will get the same number in reverse order. What's the number?
15. (solved by @Math_QED ) Let ##\mathcal{B}## be a Boolean ring with ##1##, i.e. each element of ##\mathcal{B}## is idempotent. Show that each prime ideal is maximal.
16. (solved by @lpetrich ) On a state fair is a booth where you can shoot at a square. You get ##1## point for each hit and ##2## points if you hit closer to the center than to the boundary. How big is your chance to get the extra point?
17. Let ##F_r = x^{r}\sin rA + y^{r}\sin rB + z^{r}\sin rC##, where ##x, y, z, A, B, C## are real numbers and ##A + B + C## is an integer multiple of ##\pi##. Prove that if ##F_1 = F_2 = 0## then ##F_r = 0## for all positive integers ##r##.
18. (solved by @lpetrich ) Find all three digits numbers ##x= [abc] = 100a+10b+c## such that all powers ##x^n\; , \;n\in \mathbb{N}## end on ##[...abc]##, too.
19. (solved by @lpetrich ) The product of two of the four roots of the equation ##x^4 - 18x^3 + kx^2 + 200x - 1984 = 0## is ##-32##. Find ##k##.
20. Find the maximum number of different arithmetic progressions with three terms that can be chosen from a sequence of ##n## real numbers ##a_1 \lt a_2 \lt\dots\lt a_n##.
21. (solved by @lpetrich ) Calculate curvature and torsion of the curve
$$
x\, : \,[0,a]\longrightarrow \mathbb{R}^3\, , \,x(t)=\left(t,t^2,\frac{2}{3}t^3\right)^\tau
$$
22. (solved by @lpetrich ) The teacher writes a number less than ##50,000## on the board.
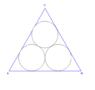
23. The Italian mathematician G.F.Malfatti presented the following in 1803, because of its degree of difficulty well-known task: Construct three circles into a given triangle so that the total area of the circles is maximal.
For the equilateral triangle, Malfatti found the solution
It wasn't until 1929 when the mathematicians Lob and Richmond showed that Malfatti had made a mistake here.
Show that there is a better solution for the equilateral triangle.
24. In which country in Europe originated this christmas custom?
Note the numbers behind your answers. If you like you can post your percentage!
25. Ten DYK Christmas gifts.
##10##: The image of Santa Claus flying his sleigh began in ##1819## and was created by Washington Irving, the same author who dreamt up the Headless Horseman.
##9##: Clement Moore's poem introduced eight more reindeer for Santa's sleigh and their names were Dasher, Dancer, Prancer, Vixen, Comet, Cupid, Duner and Blixem (for the German words for thunder (Donner) and lightning (Blitz)). These later evolved into Donner and Blitzen.
##8##: Some leave food out for Santa Claus' reindeer as Norse children did, leaving hay and treats for Odin's eight-legged horse Sleipnir hoping they would stop by during their hunting adventures. Dutch children adopted this same tradition, leaving food in their wooden shoes for St. Nicholas' horse.
##7##: America's first batch of eggnog was made in the Jamestown settlement in ##1607##. Its name comes from the word "grog", meaning any drink made with rum. Non-alcoholic eggnog is popular as well.
##6##: Between the ##16##th and ##19##th centuries global temperatures were significantly lower than normal in what was known as a "little ice age". Charles Dickens grew up during this period and experienced snow for his first eight Christmases. This "White Christmas" experience influenced his writing and began a tradition of expectation for the holidays.
##5##: The Christmas wreath was originally hung as a symbol of Jesus. The holly represents his crown of thorns and the red berries the blood he shed.
##4##: Tinsel was invented in ##1610## in Germany and was once made of real silver.
##3##: A Christmas tree is a decorated tree, usually an evergreen conifer such as spruce, pine, or fir or an artificial tree of similar appearance, associated with the celebration of Christmas. The modern Christmas tree was developed in medieval Livonia (present-day Estonia and Latvia) and early modern Germany, where Protestant Germans brought decorated trees into their homes. It acquired popularity beyond the Lutheran areas of Germany and the Baltic countries during the second half of the ##19##th century, at first among the upper classes.
##2##: The tradition of hanging stockings comes from a Dutch legend. A poor man had three daughters for whom he could not afford to provide a dowry. St. Nicholas dropped a bag of gold down his chimney and gold coins fell out and into the stockings drying by the fireplace. The daughters now had dowries and could be married, avoiding a life on the streets.
##1##: In ##1914## during World War I there was a now famous Christmas truce in the trenches between the British and the Germans. They exchanged gifts across a neutral no man's land, played football together, and decorated their shelters.
Rules:
a) In order for a solution to count, a full derivation or proof must be given. Answers with no proof will be ignored. Solutions will be posted around 15th of the following month.
b) It is fine to use nontrivial results without proof as long as you cite them and as long as it is "common knowledge to all mathematicians". Whether the latter is satisfied will be decided on a case-by-case basis.
c) If you have seen the problem before and remember the solution, you cannot participate in the solution to that problem.
d) You are allowed to use google, wolframalpha or any other resource. However, you are not allowed to search the question directly. So if the question was to solve an integral, you are allowed to obtain numerical answers from software, you are allowed to search for useful integration techniques, but you cannot type in the integral in wolframalpha to see its solution.
Hints: on demand
1. (solved by @julian ) Let ##(a_n)_{n \in\mathbb{N}}\subseteq \mathbb{R}^+## be a sequence of positive real numbers and ##A=\sum_{n=1}^\infty a_n\,.## Prove the following statements:
- (Kummer) If there is a sequence ##(b_n)_{n \in \mathbb{N}}\subseteq \mathbb{R}^+## of positive real numbers, such that there is an index ##N \in\mathbb{N}## for which ##b_{n-1}\cdot \dfrac{a_{n-1}}{a_n} - b_n \geq C## for a constant ##C>0## and all ##n>N##, then ##A## converges.
- (Kummer) If there is a sequence ##(b_n)_{n \in \mathbb{N}}\subseteq \mathbb{R}^+## of positive real numbers, such that the series ##\sum_{n=1}^{\infty}\dfrac{1}{b_n}## diverges, and there is an index ##N\in \mathbb{N}## such that ##b_{n-1}\cdot \dfrac{a_{n-1}}{a_n}-b_n \leq 0## for all ##n>N##, then ##A## diverges.
- (Bertrand) We define the sequence of real numbers by $$b_n := \left(n \cdot \left( \dfrac{a_n}{a_{n+1}}-1 \right)-1 \right)\log (n)$$ and ##B :=\lim_{n \to \infty}b_n \in \overline{\mathbb{R}}=\mathbb{R}\cup \{\,\pm \infty\,\}\,.##
Then ##A## converges if ##B>1## and diverges if ##B<1\,.##
Two mathematicians meet by chance on a plane: "Didn't you have three sons?" asks one, "how old are they?" - "The product of years is 36," is the answer, "and the sum of years is exactly today's date." "Hmm, that's not enough for me," says the colleague. "Oh, right," says the second mathematician, "I forgot to mention that my eldest son has a dog."
How old are the three sons?
All others are recommended to [/URL]https://www.physicsforums.com/threads/math-challenge-november-2018.960003/. Especially the problems 7,8,9,19,20 should be manageable, and even 15,16 look more complicated as they actually are. If you want a new problem despite of these:
2. b.) (solved by @jbstemp) The unitary matrices build a manifold, the Lie group ##SU(n)##. Calculate its tangent space at the neutral element of the group.
3. Find functions ##y(t)## and ##z(t)## which locally solve the equations
$$
\begin{cases}
e^t + \tan y(t) &= 1\\
t^2 + z(t)^3+z(t) &=0
\end{cases}
$$
in a neighborhood of ##t=0## and investigate their behavior with respect to monotony (where defined). It is sufficient to determine the functions up to a differential equation. It's a mathematical problem, so existence will do.
4. (solved by @DeathByKugelBlitz ) Find a ten digits integer with all ten digits, such that the first ##n## digits (##1\leq n \leq 10##) are divisible by ##n##. The integer should thus contain all ##10## different symbols ##0,1,2,3,4,5,6,7,8,9##.
5. Is there always a position on a floor (continuous, no holes, steps etc.) for a rectangular table with four equal legs, such that the table does not wiggle?
6. (solved by @SSequence ) Show that ##(0,1) \subset \mathbb{R}## cannot be written as a countable disjoint union of closed intervals.
7. Areas and Volumes
7.a.) (solved by @Delta2 ) Show that the paraboloid
$$P=\{\,(x,y,z)^\tau\in \mathbb{R}^3\,|\,x^2+y^2=z\, , \,x,y\in [-1,1]\,\} \subseteq \mathbb{R}^3$$
and the hyperboloid
$$H=\{\,(x,y,z)^\tau\in \mathbb{R}^3\,|\,x^2-y^2=z\, , \,x,y\in [-1,1]\,\} \subseteq \mathbb{R}^3$$
have equal areas.
7.b.) (unsloved) Bring ##M =\{\,(x,y,z)^\tau\in \mathbb{R}^3\,|\,x^2\leq y^4\leq z^8\leq 1\,\}## into a normal form and calculate its volume.
8. (solved by @Young physicist ) The table cards at a rotatable round table with 12 seats are set up for expected 12 guests. However, the persons ignore the cards and randomly distribute themselves to the seats.
Is it always possible with a single turn of the table to make sure that at least two people sit in front of their correct table cards?
9. Let ##p(x)=x^n+a_{n-1}x^{n-1}+\ldots +a_1x+a_0 \in \mathbb{R}[x]## be a polynomial where all roots are negative. Prove that $$\int_{1}^{\infty}\dfrac{1}{p(x)}\,dx$$ converges absolutely if and only if ##n>1\,.##
10. (solved by @Young physicist ) Tom bets John that he can do the following: John will recite ##99## different numbers in the range ##1 \ldots 100## (i.e. positive integers) in a random order and he will be able to find and name the only number in that range that John will have missed. Tom will do it without taking any notes. What is the best algorithmic strategy to use in order to accomplish this? Give the relevant math.
11. Let ##\emptyset \neq U \subseteq \mathbb{R}^+## be an open set, and ##x_0\in U\,.## We define the quotient logarithm of a function ##f\; : \;U \longrightarrow \mathbb{R}^+## at ##x=x_0## by
$$
f\,^-(x_0) := \lim_{x \to x_0} \dfrac{\log f(x)-\log f(x_0)}{\log x-\log x_0}
$$
Solve the 'differential equation' ##f^-=f\,.##
12. (solved by @lpetrich ) Let [itex]x_0=0,x_1=1[/itex], and [itex]x_{n+1}=n(x_n+x_{n-1})[/itex] for [itex]n\geq 1[/itex]. Find [itex]\lim_{n\to\infty}\dfrac{x_n}{n!} \quad[/itex].
13. (solved by @lpetrich ) Let ##p>q## be prime numbers such that ##p \not\equiv 1 \operatorname{mod}q##.
Prove that each group with ##pq## elements is cyclic.
14. (solved by @Young physicist ) If we multiply our five digits number by four, we will get the same number in reverse order. What's the number?
15. (solved by @Math_QED ) Let ##\mathcal{B}## be a Boolean ring with ##1##, i.e. each element of ##\mathcal{B}## is idempotent. Show that each prime ideal is maximal.
16. (solved by @lpetrich ) On a state fair is a booth where you can shoot at a square. You get ##1## point for each hit and ##2## points if you hit closer to the center than to the boundary. How big is your chance to get the extra point?
17. Let ##F_r = x^{r}\sin rA + y^{r}\sin rB + z^{r}\sin rC##, where ##x, y, z, A, B, C## are real numbers and ##A + B + C## is an integer multiple of ##\pi##. Prove that if ##F_1 = F_2 = 0## then ##F_r = 0## for all positive integers ##r##.
18. (solved by @lpetrich ) Find all three digits numbers ##x= [abc] = 100a+10b+c## such that all powers ##x^n\; , \;n\in \mathbb{N}## end on ##[...abc]##, too.
19. (solved by @lpetrich ) The product of two of the four roots of the equation ##x^4 - 18x^3 + kx^2 + 200x - 1984 = 0## is ##-32##. Find ##k##.
20. Find the maximum number of different arithmetic progressions with three terms that can be chosen from a sequence of ##n## real numbers ##a_1 \lt a_2 \lt\dots\lt a_n##.
21. (solved by @lpetrich ) Calculate curvature and torsion of the curve
$$
x\, : \,[0,a]\longrightarrow \mathbb{R}^3\, , \,x(t)=\left(t,t^2,\frac{2}{3}t^3\right)^\tau
$$
22. (solved by @lpetrich ) The teacher writes a number less than ##50,000## on the board.
- The first student finds that n is divisible by ##2##.
- The second student finds that n is divisible by ##3##.
- The third student finds that n is divisible by ##4##.
- ...
- The twelfth student finds that n is divisible by ##13##.
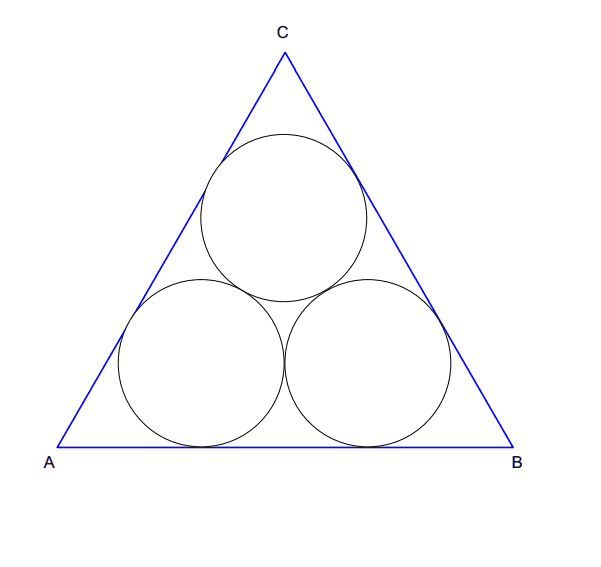
23. The Italian mathematician G.F.Malfatti presented the following in 1803, because of its degree of difficulty well-known task: Construct three circles into a given triangle so that the total area of the circles is maximal.
For the equilateral triangle, Malfatti found the solution
It wasn't until 1929 when the mathematicians Lob and Richmond showed that Malfatti had made a mistake here.
Show that there is a better solution for the equilateral triangle.
24. In which country in Europe originated this christmas custom?
Note the numbers behind your answers. If you like you can post your percentage!
- From Nikulden to Budni Vecher is lent in this country. At Christmas you can then taste Kravai, the traditional Christmas bread. The presents on Christmas Eve brings the Djado Koleda ("Grandfather Christmas").
Russia 56 - Bulgaria 27 - Christmas is Jul and a house elf named Nisse (Julenisse) is even more important in this country than Santa Claus. It is said that he lives in stables and in barns and takes care of the animals there. He likes to play a little prank on the children.
Norway 87 - Denmark 81 - The Christmas holidays are also called "beer festivals" in this country. Traditionally, they were celebrated rather quietly in the circle of the family. Even visitors were rather undesirable on the Christmas holidays, female visit on the 2nd Christmas holiday was once even considered a particularly bad omen. Christmas dinner in this country includes dishes such as roast goose, sauerkraut, potatoes, or ginger cookies.
Estonia 81 - Germany 42 - Ilex and mistletoe are important symbols of Christmas in this country, as is the robin that is most often seen on Christmas cards.
England 9 - Netherlands 3 - At Christmas, a log is burned in the fireplace and a cake shaped like a log is made, according to old customs. Otherwise, you will dine in this country rather nobly with selected delicacies. Even the smell of roasted sweet chestnuts must not be missing in the run-up to Christmas.
France 24 - Spain 67 - An absolute must at Christmas in this country is the Joulukinkku, the Christmas ham. Christmas peace is proclaimed in this country on 12/24 and deceased family members are remembered on Christmas Eve. For Christmas dinner you will be served traditional rice pudding with cinnamon, sugar and an almond, which should bring good luck.
Latvia 16 - Finland 34 - This country put the Christmas tree into the focus of Christmas for the first time. Also edible tree decoration of former times was replaced for the first time by glass balls. There are not just one, but several official gift bringers.
Germany 12 - Czech Republic 2 - ##14## days before Christmas, they turn up, the thirteen charming, but also somewhat sneaky Christmas goblins - the last one, called the "Thirteenth", will not disappear until January ##6##th. However, the children of this country have to be especially careful of the troll woman Grýla, the mother of the thirteen kobolds - who was not good, is caught by her and consumed without further ado. An absolute must at Christmas is the traditional Christmas drink Jólaöl.
Iceland 14 - Greenland 9 - Christmas is referred to in the language of this country as "Winter Festival" and Christmas Eve is the "Winter Festive Evening". On this day, according to Christian custom, the birth of Christ is celebrated, and according to ancient pagan custom, the return of the virgin of the sun. A popular Christmas ornament is Puzuri, a kind of mobile made of straw.
Latvia 22 - Poland 33 - An important pre-Christmas custom in this country is the celebration of Lucia Day: on the day of Saint Lucia, December ##13##, the eldest daughter of the house plays the "Lucia Bride" and wakes the whole family for breakfast.
On Christmas Eve, which is often called the "Dopparedan" (one-day's day), sausages, potato casserole with anchovies or Lutfisk, marinated cod are often served.
The gifts are not brought by Santa Claus or the Christkind, but the Julbock.
Sweden 23 - Lithuania 31
##27,81,81,9,24,34,12,14,22,23 \\##
##2^n+7^n+8^n+18^n+19^n+24^n=3^n+4^n+12^n+14^n+22^n+23^n \; , \;(n=0,1,\ldots ,5)##
##2^n+7^n+8^n+18^n+19^n+24^n=3^n+4^n+12^n+14^n+22^n+23^n \; , \;(n=0,1,\ldots ,5)##
25. Ten DYK Christmas gifts.
##10##: The image of Santa Claus flying his sleigh began in ##1819## and was created by Washington Irving, the same author who dreamt up the Headless Horseman.
##9##: Clement Moore's poem introduced eight more reindeer for Santa's sleigh and their names were Dasher, Dancer, Prancer, Vixen, Comet, Cupid, Duner and Blixem (for the German words for thunder (Donner) and lightning (Blitz)). These later evolved into Donner and Blitzen.
##8##: Some leave food out for Santa Claus' reindeer as Norse children did, leaving hay and treats for Odin's eight-legged horse Sleipnir hoping they would stop by during their hunting adventures. Dutch children adopted this same tradition, leaving food in their wooden shoes for St. Nicholas' horse.
##7##: America's first batch of eggnog was made in the Jamestown settlement in ##1607##. Its name comes from the word "grog", meaning any drink made with rum. Non-alcoholic eggnog is popular as well.
##6##: Between the ##16##th and ##19##th centuries global temperatures were significantly lower than normal in what was known as a "little ice age". Charles Dickens grew up during this period and experienced snow for his first eight Christmases. This "White Christmas" experience influenced his writing and began a tradition of expectation for the holidays.
##5##: The Christmas wreath was originally hung as a symbol of Jesus. The holly represents his crown of thorns and the red berries the blood he shed.
##4##: Tinsel was invented in ##1610## in Germany and was once made of real silver.
##3##: A Christmas tree is a decorated tree, usually an evergreen conifer such as spruce, pine, or fir or an artificial tree of similar appearance, associated with the celebration of Christmas. The modern Christmas tree was developed in medieval Livonia (present-day Estonia and Latvia) and early modern Germany, where Protestant Germans brought decorated trees into their homes. It acquired popularity beyond the Lutheran areas of Germany and the Baltic countries during the second half of the ##19##th century, at first among the upper classes.
##2##: The tradition of hanging stockings comes from a Dutch legend. A poor man had three daughters for whom he could not afford to provide a dowry. St. Nicholas dropped a bag of gold down his chimney and gold coins fell out and into the stockings drying by the fireplace. The daughters now had dowries and could be married, avoiding a life on the streets.
##1##: In ##1914## during World War I there was a now famous Christmas truce in the trenches between the British and the Germans. They exchanged gifts across a neutral no man's land, played football together, and decorated their shelters.
Attachments
Last edited: