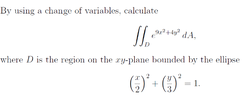Change of variables/ Transformations part 2

Click For Summary
SUMMARY

This discussion focuses on the transformation of variables in the context of mathematical expressions, specifically in the u-v plane. The recommended approach involves setting the expressions as $x = 2u$ and $y = 3v$, followed by a transition from Cartesian to polar coordinates. The discussion also highlights the parametric equations for both circles and ellipses, emphasizing their relevance in understanding transformations. The equations provided are essential for visualizing and solving problems involving these transformations.

PREREQUISITES
  • Understanding of Cartesian coordinates
  • Familiarity with polar coordinates
  • Knowledge of parametric equations
  • Basic concepts of ellipses and circles
NEXT STEPS
  • Study the derivation of parametric equations for ellipses
  • Explore the conversion process from Cartesian to polar coordinates
  • Learn about Jacobian transformations in multivariable calculus
  • Investigate applications of variable transformations in integration
USEFUL FOR

Students and educators in mathematics, particularly those studying calculus and transformations, as well as professionals working with mathematical modeling and analysis.

Joe20
Messages
53
Reaction score
1
I am not sure how I should set my u and v expressions into the u-v plane for this question.
How should I look at the expression to set u and v expressions?
 

Attachments

  • ca2.png
    ca2.png
    8 KB · Views: 121
Physics news on Phys.org
Alexis87 said:
I am not sure how I should set my u and v expressions into the u-v plane for this question.
How should I look at the expression to set u and v expressions?
You could start by letting $x = 2u$ and $y = 3v$. You might then want to make a further change, from cartesian to polar coordinates.
 
You probably know that parametric equations for a circle with radius r, centered at (0, 0), x^2+ y^2= r^2, are x= r cos(t), y= r sin(t) because x^2+ y^2= r^2cos^2(t)+ r^2 sin^2(t)= r^2(cos^2(t)+ sin^2(t))= r^2.

It should not be too much of a "jump" to see that parametric equations for the ellipse, with axes of length a and b in the x and y direction, respectively, x^2/a^2+ y^2/b^2= 1, are x= a cos(t), y= b sin(t).
 

Similar threads

Undergrad Change of variables clarification
  • · Replies 5 ·
Replies
5
Views
2K
MHB Change of variables/ Transformations
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Integral change of variables formula confusion
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Changing variables in multiple integrals
  • · Replies 1 ·
Replies
1
Views
2K
MHB How to use change of variables technique here?
  • · Replies 2 ·
Replies
2
Views
2K
Graduate Help with simplifying an integral
  • · Replies 6 ·
Replies
6
Views
2K
Undergrad Multi-dimensional Integral by Change of Variables
  • · Replies 1 ·
Replies
1
Views
2K
MHB Changing variables for defining a region
  • · Replies 2 ·
Replies
2
Views
2K
High School Question about change of variables
  • · Replies 29 ·
Replies
29
Views
5K
High School Question about the limits of integration in a change of variables
  • · Replies 2 ·
Replies
2
Views
3K