- #1
WMDhamnekar
MHB
- 376
- 28
Find the volume V inside both the sphere $x^2 + y^2 + z^2 =1$ and cone $z = \sqrt{x^2 + y^2}$
My attempt: I graphed the cone inside the sphere as follows. But I don't understand how to use the change of variables technique here to find the required volume. My answer without using integrals is volume of the cone + volume of the spherical cap = $\frac{\pi}{3} \times (\frac12) \times \frac{1}{\sqrt{2}} + \frac{ \pi}{3} *(1-\frac{1}{\sqrt{2}})^2 *(\frac{3}{\sqrt{2}}-(1-\frac{1}{\sqrt{2}}))= 0.497286611528$
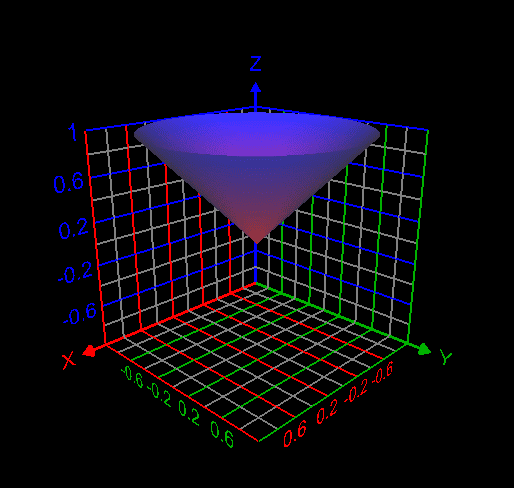

My attempt: I graphed the cone inside the sphere as follows. But I don't understand how to use the change of variables technique here to find the required volume. My answer without using integrals is volume of the cone + volume of the spherical cap = $\frac{\pi}{3} \times (\frac12) \times \frac{1}{\sqrt{2}} + \frac{ \pi}{3} *(1-\frac{1}{\sqrt{2}})^2 *(\frac{3}{\sqrt{2}}-(1-\frac{1}{\sqrt{2}}))= 0.497286611528$
Last edited: