- #1
phosgene
- 146
- 1
Homework Statement
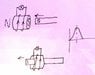
A bar magnet is dropped through a horizontal coil as shown below. An EMF is induced in the coil with the resultant voltage shown on the graph.
Explain the shape of the graph, in particular the differences in the regions marked as A, B and C.
Homework Equations
Magnetic flux = BAcosx, where B = magnetic field, A = area of wire loop and x is the angle between B and a line perpendicular to the face of the wire loop.
EMF = -N(change in magnetic flux)/(change in time), where N = thenumber of loops of wire.
The Attempt at a Solution
In segment A, there is an increase and decrease in the EMF because the bottom of the magnet is passing through the loop. The change stems from the fact that the angle of the field lines with respect to the face of the loop is constantly changing, yielding a non-zero change in magnetic flux.
In segment B, the field lines are perpendicular to the loop and the angle doesn't change, thus there is no net change in magnetic flux and the EMF does not increase.
Segment C shows a change in EMF for the same reason as section A, however, it is more spiked and brief. This is due to the bar magnet moving faster due to gravity...making the change in magnetic flux more rapid.
I drew a picture which shows which sections of the magnet product which changes in EMF according to the segment (picture of magnet and field lines stolen from google, hope this doesn't break any rules!):
Am I right here?