How to obtain correct negative sign in calculation of motional emf?

[zenterix]

Homework Statement

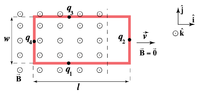
A rectangular conducting coil of length $l$, height $h$, and resistance $R$ is moving parallel to the $(x,y)$ plane at a constant velocity $\vec{v}=v_0\hat{i}$ as shown below. It continues to move through a region containing a uniform magnetic field of magnitude $B_0$. The magnetic field is in the $-\hat{k}$ direction and is confined in the region $0\leq x\leq 3l$. Consider the unit normal to the surface enclosed by the loop to be in the same direction as the magnetic field, $\hat{n}=-\hat{k}$.

Relevant Equations

Calculate $\mathcal{E}$ and $I$, the induced emf and the current in the loop, at the instant when the loop is entering the region of magnetic field. A clockwise current is positive. A counterclockwise current is negative.

My issue is with the signs.

We have

$$\mathcal{E}=\oint \vec{v}\times\vec{B}\cdot d\vec{s}$$

$$=\oint v_0\hat{i}\times B_0(-\hat{k})\cdot dy\hat{j}$$

$$=\int_0^h v_0B_0\hat{j}\cdot dy \hat{j}$$

$$=v_0Bh$$

Now, apparently, the sign should be negative.

Intuitively, the magnetic force on any positive charge in the loop that is in the magnetic field points up. The charges on the right vertical portion of the loop move up and we have a counterclockwise current.

The current is $I=\frac{\mathcal{E}}{R}$.

At what point in the equations above do I have an incorrect sign? In other words, how do I get a negative sign into the calculation of $\mathcal{E}$?

One thing I just thought about is a law that I am just coming across. Faraday's law.

$$\mathcal{E}=-\frac{d\Phi_B}{dt}$$

Where $\Phi_B$ is the magnetic flux through the loop.

Let $x(t)$ be the x-coordinate of the right side of the loop relative to the start of the portion with the magnetic field on the left side of the picture above.

$$\Phi(t)=\iint_{loop}\vec{B}\cdot d\vec{A}$$

$$=B_0hx(t)$$

Then, $\mathcal{E}=-B_0hv_0$.

This seems to work out. But how do I get the correct sign when I compute the emf directly?

 

[kuruman]

According to Faraday's Law $$\text{emf}=\oint \mathbf E\cdot d\mathbf l=-\frac{d}{dt}\int \mathbf B \cdot~\mathbf{\hat n}~dA.$$To use this, you need to orient the loop, i.e. decide which way unit vector $\mathbf{\hat n}$ is positive. Then the sense of integration in the closed loop integral on the left-hand side is to be performed following the right-hand rule.

Let's see how this works. Using your diagram, I pick $~\mathbf{\hat n}=\mathbf{\hat k}.$ Then positive circulation in the loop is counterclockwise and negative clockwise.

Look at the loop (solid line) on the far left. $$\mathbf B \cdot~\mathbf{\hat n}=B(-\mathbf{\hat k})\cdot \mathbf{\hat k}=-BA$$For a uniform magnetic field we can write $$\begin{align}\text{emf}=\oint \mathbf E\cdot d\mathbf l=+\frac{d}{dt}(BA)=B\frac{dA}{dt}.\end{align}$$The flux is positive and increasing on the right-hand side ($\dfrac{dA}{dt}>0.$) This means that the integral is positive which implies counterclockwise circulation and current.

Look at the loop in the middle. Here the flux is not changing so there is no circulation.

Look at the loop on the far right. Here $\dfrac{dA}{dt}<0$ which means that the integral is negative and implies clockwise circulation and current.

Do you see how it works?

 

[BvU]

Fwiw: I can always fall back on the expression for the Lorentz force to get the correct sign from first principle. (You do need to know how to do a cross product, however )

$\$