Characteristic Impedance of a coaxial cable

[EEuser]

Homework Statement

Why are coaxial cables designed for a 50 ohms characteristic impedance?

(a) Find the characteristic impedance of a coaxial cable for maximum power handling. Hint:
consider the trade-off between breakdown voltage and power. For the breakdown voltage
write an expression for the maximum electric field within the dielectric in terms of V and a,
b where a and b are the radii of the inner conductor and outer conductor, respectively.

(b) Next, determine the characteristic impedance of minimum attenuation. The attenuation constant simplifies to: attenuation constant= R/(2*Z0) (see image 1 below) in the low-loss case with zero dielectric loss. Due to the skin effect the current in the conductor will be confined to flow in a thin cylinder at the periphery of the inner conductor. The width of this thin cylinder is given as (see image 2 below)

Relevant Equations

see below for images of equations

Image 1:

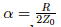Image 2:

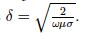
I am attempting to learn about transmission lines and am having problems with this homework problem.

• For part a, I have derived an equation for the maximum electric field within the dielectric. I came up with:
  
  with r being the radius and the electric field decreasing with increased radius r. I am not sure how this equation is to help in determining the characteristic impedance of a coaxial cable for max power handling, nor am I sure how considering the "trade-off between breakdown voltage and power" will help.
• For part b, I understand all equations and their origins, but I am not sure how to use this information to determine the characteristic impedance of minimum attenuation. I know that the typical equation for characteristic impedance is as follows:
  

Any assistance would be greatly appreciated.

 

[trurle]

• For part a, I have derived an equation for the maximum electric field within the dielectric. I came up with: View attachment 253635with r being the radius and the electric field decreasing with increased radius r. I am not sure how this equation is to help in determining the characteristic impedance of a coaxial cable for max power handling, nor am I sure how considering the "trade-off between breakdown voltage and power" will help.

You should use only maximal field. As soon as dielectric break in maximal field (i.e. on surface of inner conductor) it turns into conductor and breakdown propagates to outer sheaf.

• For part b, I understand all equations and their origins, but I am not sure how to use this information to determine the characteristic impedance of minimum attenuation. I know that the typical equation for characteristic impedance is as follows:View attachment 253636

Any assistance would be greatly appreciated.

You should assume a fixed output load. Attenuation will be product of cable loss and reflection loss.