- #1
Leonid92
- 45
- 2
- TL;DR Summary
- Basics of RF coil development for MRI
Hi all,
I'm trying to understand basics of radiofrequency (RF) coil development for magnetic resonance imaging (MRI).
For example, the problem is to develop simple surface single-loop RF coil tuned to 100 MHz.
In program Coil32, I set the following parameters:
diameter of the loop D = 20 mm;
wire diameter d = 2 mm;
working frequency = 100 MHz;
material of wire = copper.
The program calculates inductance of one turn loop coil and coil constructive Q-factor:
inductance = 0.033 uH (microhenries);
coil constructive Q-factor = 792.
Then, using the same program, I calculate external capacitance ( formula f = 1/[2π*(LC)^(1/2)] is used ):
external capacitance = 76.758 pF.
Moreover, the program calculates characteristic resistance of the LC circuit:
characteristic resistance ρ = 20.735 Ohm.
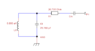
I don't understand, what is characteristic resistance and how can I depict this quantity in scheme of the RF coil. I assumed that characteristic resistance can be represented as a resistor with R1 = 20.735 Ohm. Is it right? Please find attached the scheme of the RF coil.
It is known that RF coils should be connected to MRI system using coaxial cable with impedance Z = 50 Ohm. From the scheme, one can see that there are two capacitors - tuning and matching. Tuning capacitor Ct is connected to the inductor in parallel, and matching capacitor Cm is placed between R1 and power source P1. How can I calculate capacitance of the matching capacitor Cm?
Can I use 50 Ohm coaxial cable of arbitrary length or should I calculate the length of the coaxial cable too?
I'm trying to understand basics of radiofrequency (RF) coil development for magnetic resonance imaging (MRI).
For example, the problem is to develop simple surface single-loop RF coil tuned to 100 MHz.
In program Coil32, I set the following parameters:
diameter of the loop D = 20 mm;
wire diameter d = 2 mm;
working frequency = 100 MHz;
material of wire = copper.
The program calculates inductance of one turn loop coil and coil constructive Q-factor:
inductance = 0.033 uH (microhenries);
coil constructive Q-factor = 792.
Then, using the same program, I calculate external capacitance ( formula f = 1/[2π*(LC)^(1/2)] is used ):
external capacitance = 76.758 pF.
Moreover, the program calculates characteristic resistance of the LC circuit:
characteristic resistance ρ = 20.735 Ohm.
I don't understand, what is characteristic resistance and how can I depict this quantity in scheme of the RF coil. I assumed that characteristic resistance can be represented as a resistor with R1 = 20.735 Ohm. Is it right? Please find attached the scheme of the RF coil.
It is known that RF coils should be connected to MRI system using coaxial cable with impedance Z = 50 Ohm. From the scheme, one can see that there are two capacitors - tuning and matching. Tuning capacitor Ct is connected to the inductor in parallel, and matching capacitor Cm is placed between R1 and power source P1. How can I calculate capacitance of the matching capacitor Cm?
Can I use 50 Ohm coaxial cable of arbitrary length or should I calculate the length of the coaxial cable too?