Charging a metal plate/piece of metal with capacitor

[vhb mo]

Hi all,
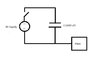
I have a question about charging a meta plate or a piece of metal with a capacitor. I need to charge a plate to negative or positive and search for some methods. I know charging by Conduction, Friction and Induction. I would like to use another method. I want to charge a capacitor (E.g. 1000 uF) and then connect the negative (or positive) pin to the metal plate or a piece of metal. In this case I think the the metal or plate should be negatively (or positively) charged. Can some one tell me is this way correct? In this case does that metal (or plate) charge?

Thanks

 

[BvU]

Hi mo,

Answer: yes, provided you do something sensible with the other 'pin' Can you understand what ? Make a sketch of the situation.

 

[vhb mo]

Hi mo,

Answer: yes, provided you do something sensible with the other 'pin' Can you understand what ? Make a sketch of the situation.

Thanks for your response, The other pin should be connected to ground. Am I right?

 

[vhb mo]

Thanks for your response, The other pin should be connected to ground. Am I right?

I did like the attached pic. The voltage of DC power supply is 30 v. I think I should increase the voltage to transfer more charges.

 

[BvU]

Thanks for your response, The other pin should be connected to ground. Am I right?

Yes. And then the metal plate gets a potential wrt ground. BAsically you are then connecting two capacitors in parallel. Since the capacity of a metal plate wrt ground is generally pretty small (1 m² at 1 cm from ground = 0.09 $\mu$F) the voltage remaining on capacitor and plate will be a large fraction ($C_1\over C_1+C_2$) of the original voltage on the capacitor.

Picture I had in mind:

 

[vhb mo]

Yes. And then the metal plate gets a potential wrt ground. BAsically you are then connecting two capacitors in parallel. Since the capacity of a metal plate wrt ground is generally pretty small (1 m² at 1 cm from ground = 0.09 $\mu$F) the voltage remaining on capacitor and plate will be a large fraction ($C_1\over C_1+C_2$) of the original voltage on the capacitor.

Picture I had in mind:

View attachment 113346

Thanks, How about choosing a small cap close to the plate capacitor. E.g. 100 nF cap. I think this can transfer more charges to the plate.

 

[BvU]

Length of connections doesn't come into the calculation !

 

[vhb mo]

Length of connections doesn't come into the calculation !

No No, I do not talk about the length. I talk about the amount of the capacitors. I mean that I change the amount of charged capacitor (100 nF) to the value close to the capacity of the plate to ground (90 nF).

 

[BvU]

How about choosing a small cap close to the plate capacitor

Ah, you meant:
choosing a small capicitor with a capacitance close to the plate capacitance

Well, the case is:

Before connecting you have a charge $Q = C_1V_0$ if $C_1$ on the capacitor if $C_1$ is its capacitance.

After connecting, that charge is distributed over capacitor and plate until the potential $V_1$ on capacitor and plate is identical (they are connected by a wire), so if $C_{\rm plate}$ is the capacitance of the plate, you have $$ C_1 V_0 = Q = C_1 V_1 + C_{\rm plate} V_1 $$ whereby $V_1 = V_0 {C_1\over C_1+ C_{\rm plate} }$ so $$ Q_{\rm plate} = C_{\rm plate} V_1 = C_{\rm plate} {V_0 C_1 \over C_1+ C_{\rm plate} } \approx {C_{\rm plate} V_0} \quad {\rm if }\ \ C_1 >> C_{\rm plate} $$
whereas this would be $\approx C_{\rm plate} V_0/2 \quad {\rm if }\ \ C_1 \approx C_{\rm plate}$

 

[Baluncore]

How you should charge the plate will be decided by why you want to charge it.
Remember that capacitance, C = Q / V.

To place the maximum charge, Q = C·V on the plate, you need to maximise C and V. So use the maximum plate area with the minimum gap to ground, then charge it with the highest voltage available.

For maximum voltage, V = Q / C, you need to maximise Q while minimising C. But there is a parametric multiplication trick that can be used. Once the plate is charged, the charge will remain fixed because it has no where to flow, then dV = Q / dC. So charge the plate as before, with the minimum separation to the maximum voltage, then increase the separation of the plate from ground, which will reduce the capacitance and so multiply the voltage beyond that used initially to charge it.

 

[BvU]

Balun's advice is good. But now I wonder why

I need to charge a plate

i.e. what's the goal of this exercise ?

 

[vhb mo]

Ah, you meant:
choosing a small capicitor with a capacitance close to the plate capacitance

Well, the case is:

Before connecting you have a charge $Q = C_1V_0$ if $C_1$ on the capacitor if $C_1$ is its capacitance.

After connecting, that charge is distributed over capacitor and plate until the potential $V_1$ on capacitor and plate is identical (they are connected by a wire), so if $C_{\rm plate}$ is the capacitance of the plate, you have $$ C_1 V_0 = Q = C_1 V_1 + C_{\rm plate} V_1 $$ whereby $V_1 = V_0 {C_1\over C_1+ C_{\rm plate} }$ so $$ Q_{\rm plate} = C_{\rm plate} V_1 = C_{\rm plate} {V_0 C_1 \over C_1+ C_{\rm plate} } \approx {C_{\rm plate} V_0} \quad {\rm if }\ \ C_1 >> C_{\rm plate} $$
whereas this would be $\approx C_{\rm plate} V_0/2 \quad {\rm if }\ \ C_1 \approx C_{\rm plate}$

How you should charge the plate will be decided by why you want to charge it.
Remember that capacitance, C = Q / V.

To place the maximum charge, Q = C·V on the plate, you need to maximise C and V. So use the maximum plate area with the minimum gap to ground, then charge it with the highest voltage available.

For maximum voltage, V = Q / C, you need to maximise Q while minimising C. But there is a parametric multiplication trick that can be used. Once the plate is charged, the charge will remain fixed because it has no where to flow, then dV = Q / dC. So charge the plate as before, with the minimum separation to the maximum voltage, then increase the separation of the plate from ground, which will reduce the capacitance and so multiply the voltage beyond that used initially to charge it.

Thanks both, Well I think to another way. Preparing another layer and make a capacitor to charge the both layers and then separate them to have 2 charged layers. Please see the attached pic. In this case the amount of charges on the plates goes higher because the amount of capacitance goes higher.

Balun's advice is good. But now I wonder why
i.e. what's the goal of this exercise ?

I am a technology developer of a company and our technology should be improved to fulfill the market requirements. :)

 

[BvU]

I am a technology developer of a company and our technology should be improved to fulfill the market requirements. :)

Of course, I should have known
Is it clear Balun's recipe gets you lots of potential, whereas your idea gets you lots of charge ? From your wording I suppose the latter is the goal, right ?

As the wise man said: it's all about Q = CV and keeping an eye on which of these is conserved under a change in the configuration

 

[vhb mo]

Of course, I should have known
Is it clear Balun's recipe gets you lots of potential, whereas your idea gets you lots of charge ? From your wording I suppose the latter is the goal, right ?

As the wise man said: it's all about Q = CV and keeping an eye on which of these is conserved under a change in the configuration

Yes you are write, I will test it tomorrow and see the results. The problem is how to convince the business part to do it because they are always saying keep the price issues in your mind. Well I should remove the bottleneck! and it brings some costs. let's see. ;)