Checking if f(x)=g(x)+h(x) is onto

[Titan97]

This is picture taken from my textbook.

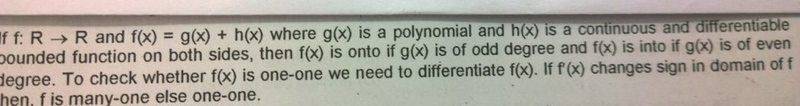
I understood the last two statements "To check whether..". A function is one if its strictly increasing or decreasing. But I am not able to understand the first statement. Polynomials are continuous functions. Also, a continuous function ± discontinuous function may be continuous. (eg: {x}+[x]) So why should h(x) necessarily be a continuous function?

 

[mfb]

It does not make any statement for discontinuous functions. Sure, there are discontinuous h(x) that would still work, but not in the general case.

Unrelated:
The sum of a continuous function and a discontinuous function is discontinuous. Your example sums two discontinuous functions.

 

[Titan97]

So h(x) has to be continuous. (I got cinfused while typing). But what makes f(x) onto?

 

[mfb]

What do you know if g(x) is a polynomial of odd degree?
Does the information about continuity and bounds change if you add a bound continuous function?

 

[Titan97]

For polynomials of odd degree, the range is (-∞,∞). If h(x) is only defined ∀ x∈[a,b], then f(x)=g(x)+h(x) is only defined ∀ x∈(a,b).

 

[mfb]

That's not how "bounded function" is meant here. Its function values are limited, not its domain.

 

[Titan97]

The continuity won't change if you add such a function like x+sinx

 

[micromass]

Given a polynomial of odd degree $P(x)$. Think about
$$\lim_{x\rightarrow +\infty} P(x)~\text{and}~\lim_{x\rightarrow -\infty} P(x)$$
Can those be equal? Can you give an example when those limits will be equal?

 

[Titan97]

They won't be equal

 

[micromass]

So what will they be concretely? Can you deduce from that that the function $P(x)$ is onto?

 

[Titan97]

Yes.

 

[micromass]

OK, then the general case shouldn't be too difficult either.