MHB Checking Proof of Theorem 6.2.8 Part (ii)

[Math Amateur]

I have completed a formal proof of D&K Theorem 6.2.8 Part (ii) ... but I am unsure of whether the proof is correct ... so I would be most grateful if someone could check the proof and point out any errors or shortcomings ...

Theorem 6.2.8 reads as follows:

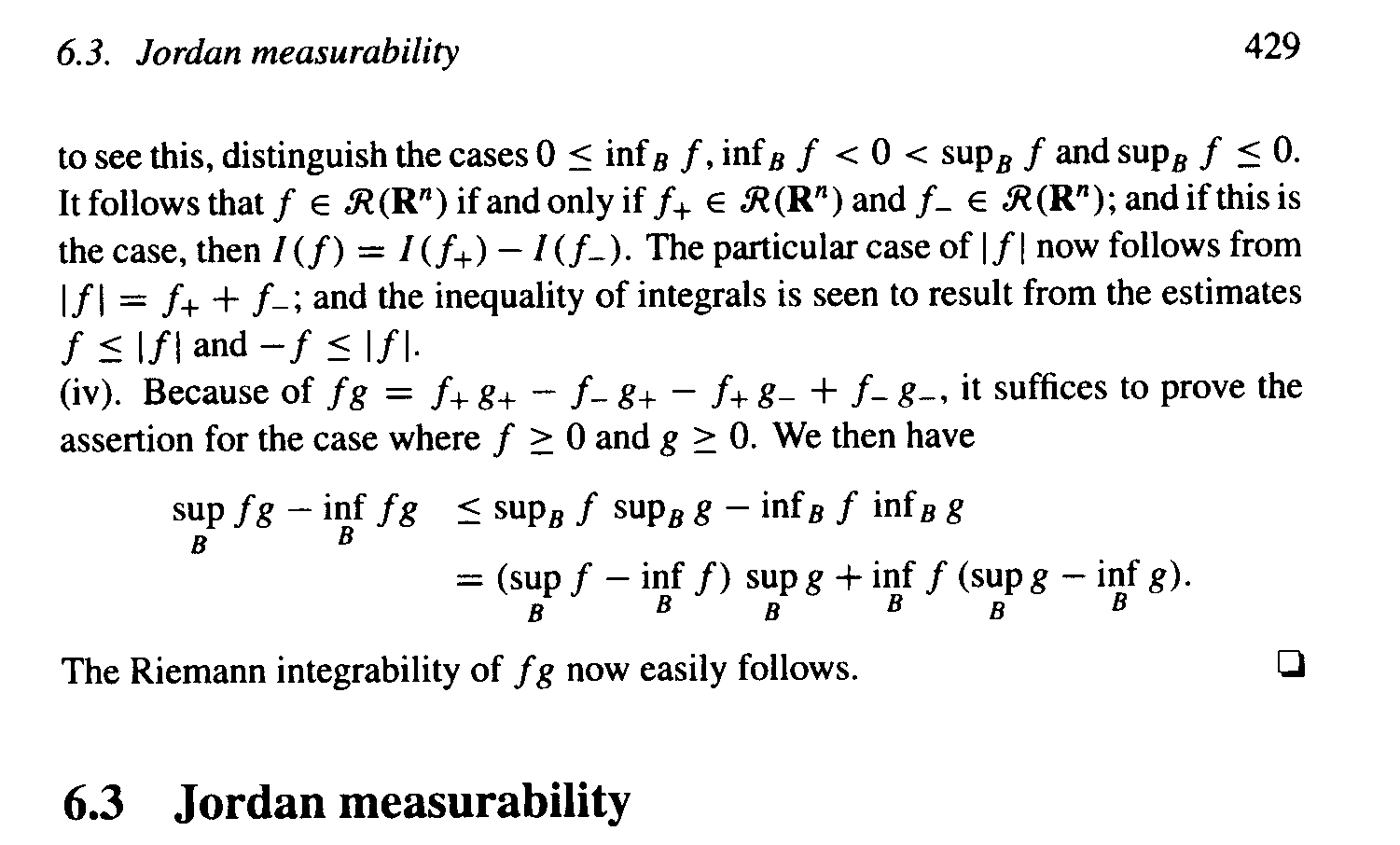
Attempted Proof of Theorem 6.2.8 Part (ii)
We have to show:

[math] f \leq g \Longrightarrow I(f) \leq I(g) [/math]

where

[math] I(f) = \int_{ \mathbb{R^n} } f(x) dx = \int_{B} f(x) dx [/math]

and

[math] I(g) = \int_{ \mathbb{R^n} } g(x) dx = \int_{B} g(x) dx [/math]
Proof:

Given a partition [math] \mathscr{B} \text{ of } B [/math] we have

[math] \overline{S} (f, \mathscr{B} ) \ = \ \sum_{j \in J} \ \sup_{ x \in B_j} \ f(x) dx \text{ vol}_n (B_j) [/math]

and

[math] \overline{S} (g, \mathscr{B} ) \ = \ \sum_{j \in J} \ \sup_{ x \in B_j} \ g(x) dx \text{ vol}_n (B_j) [/math]Now, since [math] f(x) \leq g(x) \ \ for all x \in B [/math] we have

[math] \overline{S} (f, \mathscr{B} ) \ \leq \ \ \overline{S} (g, \mathscr{B} ) [/math]it follows that:

[math] \overline{ \int_{B} } f(x) dx = \text{ inf} \ \{ \overline{S} (f, \mathscr{B} ) \ \ | \ \ \mathscr{B} \text{ is a partition of } B \} \ \ \leq \ \ \text{ inf} \ \{ \overline{S} (g, \mathscr{B} ) \ \ | \ \ \mathscr{B} \text{ is a partition of } B \} \ = \ \overline{ \int_{B} } g(x) dx [/math] ... ... ... ... ... (1)Similarly ... ... [math] \underline{ \int_{B} } f(x) dx \leq \underline{ \int_{B} } g(x) dx [/math] ... ... ... ... ... (2)(1), (2) [math] \Longrightarrow \int_{B} f(x) dx \leq \int_{B} g(x) dx [/math] ... ...

... ... that is ... ...

[math] I(f) \leq I(g) [/math]
Could someone please check my proof for correctness ... and point out any errors, shortcomings and areas needing improvement ...

Peter

NOTE:

It may help readers of the above post to have access to D&K Section 6.2 so as to be able to check the way the authors present the theory and also to check notation so I am providing a scan of section 6.2 as it reads before Theorem 6.2.8 ... see below

Hope that helps ...

Peter

 

[GJA]

Hi Peter

Proof looks good. Two small comments:

1. It is true that since both $f$ and $g$ are bounded with compact support, it is possible to select a single rectangle $B$ for which $f(x) = g(x) = 0$ for $x\notin B$. I think to improve the rigor of your proof, it is worth saying something like this at the beginning of the argument because, technically speaking, $f,g\in\mathcal{R}(\mathbb{R}^{n})$ imply there are rectangles $B_{f}$ and $B_{g}$ specific to $f$ and $g$, respectively. Again, your proof is rigorous enough in my eyes, but I do think emphasizing this point would improve the precision a bit.
2. When you say "Similarly ... ... [math] \underline{ \int_{B} } f(x) dx \leq \underline{ \int_{B} } g(x) dx [/math] ...," you are correct that an analogous argument would establish the inequality for the lower Riemann integrals. However, you do not need to actually mention this. Can you see why? By assuming $f,g\in\mathcal{R}(\mathbb{R}^{n})$, what do we know about the upper and lower Riemann integrals?

Hopefully these comments help. Let me know if the question I've posed in part 2 above is unclear.

 

[soloenergy]

Hello Peter,

Thank you for sharing your proof with us. I have read through it and I think it is a solid attempt at proving Theorem 6.2.8 Part (ii). However, there are a few areas that I think could use some improvement.

Firstly, I would suggest defining the terms "partition" and "volume" in your proof, as not all readers may be familiar with these concepts. This will make your proof more accessible to a wider audience.

Secondly, I noticed that in your proof, you use the notation \overline{\int_B} and \underline{\int_B} for the upper and lower integrals, respectively. However, in the statement of the theorem, the notation used is I(f) and I(g). It would be clearer if you use the same notation in your proof to avoid confusion.

Lastly, I would suggest providing a brief explanation or justification for each step in your proof, especially for equations (1) and (2). This will help the reader follow your thought process and understand the reasoning behind each step.

Overall, I think your proof is well-structured and easy to follow. Keep up the good work!