Circular Motion, Massless String - Swinging Rock

[Shaku]

1. Homework Statement :
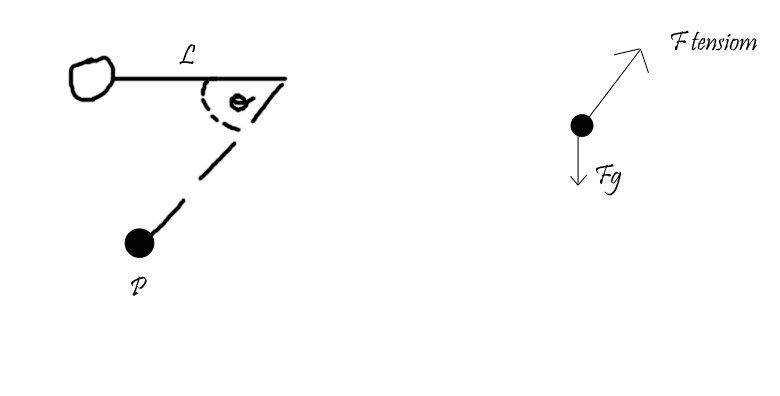
A rock of mass m is attached to a string of negligible mass and length L. The rock is released from rest from a horizontal position. When the rock is at point P, the string attached to the rock makes an angle θ with the horizontal.

In terms of the quantities, m, L, θ and any necessary constants:
a. Draw a free-body diagram of the rock at point P.
b. Find the speed of the rock at point P.
c. Find the tension in the string at point P.
d. Find the tangential acceleration of the rock at point P.

Homework Equations

Newton's Laws
Energy equations
Tangential Acceleration = (angular velocity/time)

The Attempt at a Solution

I originally tried using only Newton's laws to solve this (I went through and solved the entire problem), only to realize that it was not in the correct quantities (m, L, θ).

I thought of re-doing this problem using energy, but I'm not entirely sure how to go about doing that. I also figured that if I DID use energy to solve this, I would be lacking a time variable which I would have needed in part D.

Putting up my work here seems pointless since it's wrong, but I'll give a general outline of what I did:
1) Drew FBD of rock at point P.
2) Found the velocity in the X and Y directions using F_net = mv^2/r and used the Pythagorean theorem to find the speed (this had a tension term in it, which should not be a part of the answer...).
3) Rewrote the expression I got for velocity in terms of tension to find the tension (this had velocity in it, which should not be a part of the answer...).
4) Found tangential acceleration using w/t, where w = the velocity I solved for earlier, and t=t (t should not be a part of the answer...).

I'd appreciate if someone could give an outline similar to the one above of what I should have done to solve this problem correctly with the correct quantities (m, L, θ). Please include the equation and concept that I should use (this is more or less for understanding mainly), as well a general idea of what I should end up with.

Diagram and Free-Body Diagram:

 

[haruspex]

I don't understand how you would have used F = mv²/r to find the speed. Use energy to find the speed, then use that equation to find the tension.

 

[Shaku]

I don't understand how you would have used F = mv²/r to find the speed.

I used
F_netx = mgsinθ
F_nety = T - mgcosθ

plugged those into two separate equations
mgsinθ = mv_x^2/r
and
T-mgcosθ=mv_y^2/r

solved for v and found
$\sqrt{LgSinθ}$ = v_x
$\sqrt{L(T-mgCosθ)/m}$ = v_y

then used the Pythagorean Theorem to find V.

Use energy to find the speed, then use that equation to find the tension.

K_i + U_i = K_f + U_f

I know that the initial kinetic energy is 0, so:

U_i = K_f + U_f

mgh_i = $\frac{1}{2}$mv² + mgh_p

so:

gh_i = $\frac{1}{2}$v² + gh_p

if we solve this for V, we get:

v = √(2g(h_i - h_p))

But this is still in terms of h... We're only allowed to have the answers in m, L, θ, and necessary constants.

EDIT: I was looking at an older problem from my notes, and noticed that we used (mg*radius) instead of h. That was a cart on a circular track, so I'm not sure if the same concept applies to tension.

If it does, we would have:
v = $\sqrt{2gL}$

 

[haruspex]

I used
F_netx = mgsinθ

Are you taking x as horizontal and y as vertical? If so, you only seem to have tension as vertical. If not, I can't make much sense of your other equations.

F_nety = T - mgcosθ

plugged those into two separate equations
mgsinθ = mv_x^2/r
and
T-mgcosθ=mv_y^2/r

solved for v and found
$\sqrt{LgSinθ}$ = v_x
$\sqrt{L(T-mgCosθ)/m}$ = v_y

then used the Pythagorean Theorem to find V.

ok, that's finding v in terms of T, but you still need to use energy to find v without using T, then use the above to find T. So really you have not found v above. That's what confused me in your description of what you've done. Even so, your equation is wrong. You should have T-mg sin(θ) = mv²/L.

v = √(2g(h_i - h_p))

But this is still in terms of h... We're only allowed to have the answers in m, L, θ, and necessary constants.

So express the heights in terms of L and theta.

 

[Shaku]

Are you taking x as horizontal and y as vertical? If so, you only seem to have tension as vertical. If not, I can't make much sense of your other equations.ok, that's finding v in terms of T, but you still need to use energy to find v without using T, then use the above to find T. So really you have not found v above. That's what confused me in your description of what you've done. Even so, your equation is wrong. You should have T-mg sin(θ) = mv²/L.

Ah, thanks for catching that. I had my axis set up with with tension along the y-axis, so I got confused when I determined the sin/cos values.

So express the heights in terms of L and theta.

I currently have
v = $\sqrt{2gL}$

How would I factor the angle into that?

Would it be
v = $\sqrt{2g*Lsinθ}$? (I just looked at the triangle the angle creates, and I'm guessing that this -should- be the correct equation, but I'm not sure).

 

[haruspex]

Would it be
v = $\sqrt{2g*Lsinθ}$?

Yes.

 

[Shaku]

Alright, cool!

So now that I have the velocity, I can solve for the tension by using the same equation as I used to find velocity before, but this time solving it for T (*note, this is with corrections):

$\sqrt{LgCosθ}$ = v_x
$\sqrt{L(T-mgSinθ)/m}$ = v_y

So, solving for V I'd get:
V = $\sqrt{LgCosθ + (L(T-mgSinθ)/m)}$

Solving that for T, I get:
T = ((V²m-2gCosθ)/L) + mgCosθ

Plugging in the velocity I found earlier, I get:
T = (((2g*Lsinθ)m-2gCosθ)/L) + mgCosθ

Is this correct?

I started working on the next part of the problem, "Find the tangential acceleration of the rock at point P." and I was confused about how to go about doing this. Is the velocity I found the angular velocity? Also, how do I find the time in terms of m, L, and θ (I'm confused on what equation to use)?

I found that:
a_t = r(angular velocity/t)
a_t = L($\sqrt{(2g*Lsinθ)}$/t) -- But I don't know what equation to use to solve for t.

 

[haruspex]

$\sqrt{LgCosθ}$ = v_x
$\sqrt{L(T-mgSinθ)/m}$ = v_y

I don't understand how you get those equations. It will be easier to work with v as a whole, not splitting it into components.

 

[Shaku]

I don't understand how you get those equations.

I'm trying to use F_net = mv^2/r. The net force in the x direction is mgCosθ
and the net force in the y direction is T - mgSinθ. I plugged each respective net force into the equation to solve for v_x and v_y, and then took the Pythagorean theorem to find V as a single vector instead of it being split into components.

It will be easier to work with v as a whole, not splitting it into components.

How do I do this considering I have motion in two dimensions? I don't know how to set up my equation...

F_net = mv²/L
F^T+F^G = mv²/L
Since my y-axis is along the tension:
T - mgSinθ + mgCosθ = (mv²/L)
T = (mv²/L) + mgSinθ - mgCosθ
then plugging velocity in:
T = m(2g*Lsinθ) + mgSinθ - mgCosθ

Is that how I'm supposed to do this without splitting it up into components?

 

[haruspex]

I'm trying to use F_net = mv^2/r. The net force in the x direction is mgCosθ and the net force in the y direction is T - mgSinθ.

That's true if y is radial and x tangential. But in that case v_y = 0.

 

[Shaku]

That's true if y is radial and x tangential. But in that case v_y = 0.

This is how I have it set up:

From this, how do I set up my equation to find the tension without breaking it into components?

Forces in the Y direction:
T-mgSinθ

Forces in the X direction:
mgCosθ

 

[haruspex]

OK, that's what I deduced from your force equation. But notice that with these coordinates, at a given instant, the velocity is entirely in the x direction. T - mg sin(θ) = mv²/L. I should also have pointed out that you keep writing Fnet = mv²/L. That would be true if v were constant magnitude, but there is also tangential acceleration here. So you should write Fnet_y = mv²/L.

 

[Shaku]

OK, that's what I deduced from your force equation. But notice that with these coordinates, at a given instant, the velocity is entirely in the x direction.

Ohhh, okay. That makes sense now. Since there is no velocity at any point in the path, that would mean there is also no acceleration, so:

Fnet_y = 0
T - mgSinθ = 0,

thus Fnet_y=mv²/r would just be 0.

T - mg sin(θ) = mv²/L. I should also have pointed out that you keep writing Fnet = mv²/L. That would be true if v were constant magnitude, but there is also tangential acceleration here. So you should write Fnet_y = mv²/L.

Since Fnet_y is 0,
Fnet_x = F_net

So
mgCos = mv_x²/L

... But I'm pretty sure I did something wrong here because there is no tension so I can't solve for it.

 

[haruspex]

Ohhh, okay. That makes sense now. Since there is no velocity at any point in the path, that would mean there is also no acceleration, so:

No! At a given instant, the velocity is in the tangential (x) direction, but that direction keeps changing. There is acceleration in both the tangential direction (the speed increases) and the radial direction (centripetal).
T - mg sin(θ) = mv²/L.
Use the expression you have for v from considering energy.

 

[Shaku]

No! At a given instant, the velocity is in the tangential (x) direction, but that direction keeps changing. There is acceleration in both the tangential direction (the speed increases) and the radial direction (centripetal).

Okay, that clarifies things after making a visualization of the situation.

T - mg sin(θ) = mv²/L.
Use the expression you have for v from considering energy.

T = (mv²)/L + mgSinθ
T = (m(2g*LSinθ)/L) + mgSinθ
T = m((2g*Lsinθ)/L + gSinθ)

 

[haruspex]

T = m((2g*Lsinθ)/L + gSinθ)

Yes, but you can simplify that a little.

 

[Shaku]

I was just looking over my work, and I noticed that I didn't quite understand why you said T - mgsinθ was the net force in the Y direction.

If my axis was horizontal and vertical, it would be Tsinθ - mg, but I had set my axis is along the path of motion.

I'm confused how you got your angle... Could you clarify the reasoning behind this?

--
Also, as question on the side: If I had used the horizontal and vertical axis, would I just find the tension_x and tension_y and take the pythagorean theorm to find the tension?

 

[haruspex]

Unusually,theta is the angle to the horizontal, not the vertical. So the component of mg in the radial direction is mg sin theta. The component of T in that direction is T. T acts in the direction of the centripetal acceleration, while g acts the other way.

 

[Shaku]

Okay, that makes sense.

For part d, where the problem asks top find the tangential acceleration, I know that there are two equations I can use: a_t = w/t or a_t = L*alpha.

From the diagram, wouldn't it just be gCosθ? I'm not sure how to actually use these equations to get an answer though, as I don't know time nor how to get the angular velocity or alpha.

 

[haruspex]

.
For part d, where the problem asks to find the tangential acceleration, I know that there are two equations I can use: a_t = w/t or a_t = L*alpha.

From the diagram, wouldn't it just be gCosθ?

That's a third equation you can use (F=ma), so use it.

 

[Shaku]

Fnet_x = ma_t
mgCosθ = ma_t
gCosθ = a_t

Would this be the correct usage of the equations?

 

[haruspex]

Fnet_x = ma_t
mgCosθ = ma_t
gCosθ = a_t

Would this be the correct usage of the equations?

Yes.

 

[Shaku]

Alright.

One last question,
If I had used the vertical axis as my y-axis, and horizontal axis as my x-axis, would I just find the tension_x and tension_y and take the pythagorean theorm to find the tension?

Ex:
Fnet_y = Tsinθ - mg
Fnet_x = Tcosθ

T_ysinθ - mg = mv²/r
T_xcosθ = mv²/r

T_y = (mv²/r + mg)/sinθ
T_x = (mv²/r)/cosθ

T = $\sqrt{Ty^2 + Tx^2}$

 

[haruspex]

T_ysinθ - mg = mv²/r
T_xcosθ = mv²/r

It will still be true that T - mg sin θ = mv²/r. If you want to write that in terms of x and y components then you need to resolve acceleration into those components. And both the x and y accelerations will involve a centripetal term and a tangential term. Rather messier.

 

[Shaku]

Alright, I'm glad I started with the easier set of coordinates.
Thank you for all the help!