crossfacer
- 20
- 0
Circular motion-----"slipping" problem
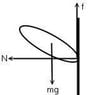
The figure attached shows a man riding a motorcycle on the rough wall of a cylindrical room. He is performing uniform circular motion and does not slide down along the wall.
If the man rides the motorcycle and performs circular motion along the rough wall without slipping, prove that the following condition must hold:
If the motorcycle does not slip,
In the solution, the answer uses:
Homework Statement
The figure attached shows a man riding a motorcycle on the rough wall of a cylindrical room. He is performing uniform circular motion and does not slide down along the wall.
If the man rides the motorcycle and performs circular motion along the rough wall without slipping, prove that the following condition must hold:
1 <= (u*v^2) / rg
where u is the coefficient of static friction, v is the speed of the motorcycle, r is the radius of the circle and g is the acceleration due to gravity.The Attempt at a Solution
If the motorcycle does not slip,
N >= mv^2 / r------------(i)
Consider vertical motion:f - mg = 0
f = mg
uN = mg
N = mg / u-------------(ii)
Substitute (ii) to (i):f = mg
uN = mg
N = mg / u-------------(ii)
mg / u >= (mv^2) / r
1 >= (uv^2) / rg
1 >= (uv^2) / rg
In the solution, the answer uses:
mg <= f-------(I)
and N = (mv^2) / r-----------(II)
But why (I) is correct when the motorcycle does not slip? If mg > f, will the motorcycle go upward? And what's wrong with my answer? Thank you so much!and N = (mv^2) / r-----------(II)
Attachments
Last edited: