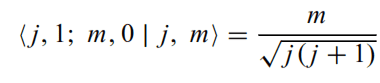SUMMARY
The discussion centers on deriving a specific Clebsch–Gordan (CG) identity, particularly in the format . Participants reference the general expression for CG coefficients, which involves Wigner 3j-symbols and angular momentum coupling. The key formula provided includes factorial expressions and conditions for summation over n, specifically for the case where j1 = j3 = j, j2 = 1, m1 = m3 = m, and m2 = 0. This identity is crucial for understanding the addition of angular momenta in quantum mechanics.
PREREQUISITES
- Understanding of Clebsch–Gordan coefficients
- Familiarity with Wigner 3j-symbols
- Knowledge of angular momentum coupling in quantum mechanics
- Basic proficiency in mathematical expressions involving factorials
NEXT STEPS
- Study the derivation of Clebsch–Gordan coefficients in detail
- Explore the properties and applications of Wigner 3j-symbols
- Learn about angular momentum coupling techniques in quantum mechanics
- Investigate advanced topics in quantum mechanics related to angular momentum
USEFUL FOR
Quantum physicists, students of quantum mechanics, and researchers focusing on angular momentum theory will benefit from this discussion.