MHB Coefficent in a infinite power series

Click For Summary
SUMMARY

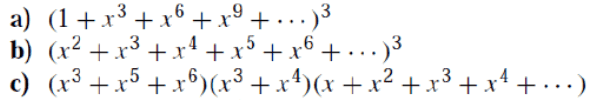
The coefficient of \(x^9\) in the given infinite power series is definitively 10. This conclusion is drawn from the combinatorial analysis of the equation \(9 = 0 + 9, 1 + 8, 2 + 7, 3 + 6, 4 + 5, 5 + 4, 6 + 3, 7 + 2, 8 + 1, 9 + 0\), which identifies 10 distinct combinations that yield the term \(x^9\). Each combination represents a unique way to sum to 9 using non-negative integers, confirming the coefficient's value.

PREREQUISITES
  • Understanding of power series and their coefficients
  • Basic knowledge of combinatorial mathematics
  • Familiarity with polynomial expressions
  • Ability to interpret mathematical equations and expressions
NEXT STEPS
  • Study combinatorial techniques for finding coefficients in power series
  • Learn about generating functions and their applications in series
  • Explore the concept of partitions in number theory
  • Investigate advanced topics in infinite series and convergence
USEFUL FOR

Mathematicians, students studying combinatorics, educators teaching power series, and anyone interested in the application of algebraic techniques to find coefficients in polynomial expressions.

pac1337
Messages
1
Reaction score
0
How do I find a coefficient of x^9 in a power series like this:
Screenshot 2021-06-03 174217.png
 
Physics news on Phys.org
For (a) 9= 0+ 9= 1+8= 2+ 7= 3+ 6= 4+ 5= 5+ 4= 6+ 3= 7+ 2= 8+ 1= 9+ 0.
There are 10 products that give $x^9$ so the coefficient is 10.
 

Thread 'My basic understanding of set theory'

If there are an infinite number of natural numbers, and an infinite number of fractions in between any two natural numbers, and an infinite number of fractions in between any two of those fractions, and an infinite number of fractions in between any two of those fractions, and an infinite number of fractions in between any two of those fractions, and... then that must mean that there are not only infinite infinities, but an infinite number of those infinities. and an infinite number of those...
View full post »

Similar threads

Undergrad Stationary time series with seasonality...
  • · Replies 8 ·
Replies
8
Views
3K
Undergrad Infinite Series of Infinite Series
  • · Replies 7 ·
Replies
7
Views
2K
Is this integral correct? (expanding the Bessel function into power series )
  • · Replies 3 ·
Replies
3
Views
809
Maximum value of Coefficient of Fibonacci Polynomial
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Time series and why would we remove seasonality and trend?
  • · Replies 10 ·
Replies
10
Views
3K
Undergrad About convergence of complex power series on the circle ##|z - z_0|=r##
  • · Replies 22 ·
Replies
22
Views
4K
Why is the Fourier coefficent calculated like this?
  • · Replies 4 ·
Replies
4
Views
1K
Undergrad Fit a non-linear function to this time series
  • · Replies 6 ·
Replies
6
Views
1K
MHB ZFC and the Axiom of Power Sets ....
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Cardinality of the Power Series of an Infinite Set
  • · Replies 19 ·
Replies
19
Views
4K