Combined linear and rotational motion question

[Dtbennett]

Homework Statement

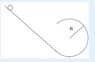
A small solid disk (r<<R), mass m = 9.3 g, rolls on its edge without skidding on the track shown, which has a circular section with radius R = 9.7 cm. The initial height of the disk above the bottom of the track is h = 30.8 cm. When the ball reaches the top of the circular region, what is the magnitude of the force it exerts on the track? (Hint: how fast is it going then?)

Homework Equations

I = 1/2MR^2

F(centripetal) = (mv^2)/r

The Attempt at a Solution

So I'm pretty sure you have to first calculate the velocity of the disk as it enters the circular part. However, I'm confused as to how as we are not provided with a time. Can you assume it is 1 second?

Then the net force must equal the centripetal force at the top of the loop, which will probably be close to zero.
And the speed of the object must match the centripetal force provided by gravity.

so making the centripital force equal to mg gives you

v= sqrt(rg)

I've gotten this far, but I have no idea where to go from here. Please help!

 

[voko]

So I'm pretty sure you have to first calculate the velocity of the disk as it enters the circular part.

You can, but why do you need to? You need the velocity at the top of the circular track, not at its bottom.

Then the net force must equal the centripetal force at the top of the loop, which will probably be close to zero.

This assumption is not based anything substantial, and so best avoided.

And the speed of the object must match the centripetal force provided by gravity.

Then you can already answer the question in the problem: zero. Does that look right to you?

 

[haruspex]

Use a conservation law.

 

[Gianf]

this problem is really tricky, I am having many problems trying to solve it

 

[Rellek]

http://en.wikipedia.org/wiki/Rotational_energy

http://en.wikipedia.org/wiki/Kinetic_energy#Rotation_in_systems

Take a look at both of these links and try to formulate your own equation. I suggest using conservation of energy. It would also be very useful to find some kind of comparison between the translational velocity of your center of mass and your tangential velocity, which is a function of $\omega$.

 

[Gianf]

Hi,
what I did was saying that mg(h-2r)=1/2mv^2 at the top of the circle. would this be correct?

 

[haruspex]

Hi,
what I did was saying that mg(h-2r)=1/2mv^2 at the top of the circle. would this be correct?

Yes.

 

[voko]

Since $r$ is taken into account for potential energy, perhaps the kinetic energy due to rotation should also be taken into account?