What actually is the centripetal acceleration formula?

[Adesh]

Homework Statement

Is centripetal force the force acting towards the Center of rotation or towards the axis of the rotation?

Relevant Equations

Centripetal Acceleration $a = \frac{v^2}{r}$.

Centripetal force is defined as the force causing the body to follow a curved path, acting towards the center and always orthogonal to the direction of motion. For uniform circular motion the formula for centripetal acceleration is $$a_c = \frac{v^2}{r}$$.

But my understanding of centripetal acceleration began to shake when I confronted this problem:
A smooth wire of length $2 \pi r$ is bent into a circle and kept in a vertical plane. A bead can slide smoothly on the wire. When the circle is rotating with angular speed $\omega$ about the vertical diamteter $AB$, as shown in figure, the bead is at rest with respect to the circular ring at position P as shown. Find the value of $\omega ^2$..

I attempted to solve it this way: at point P there is gravitational acceleration $a_g = - g ~\hat{j}$. Now, I thought for point P to be in static situation (w.r.t. to the circle) this downward acceleration must be cancelled.

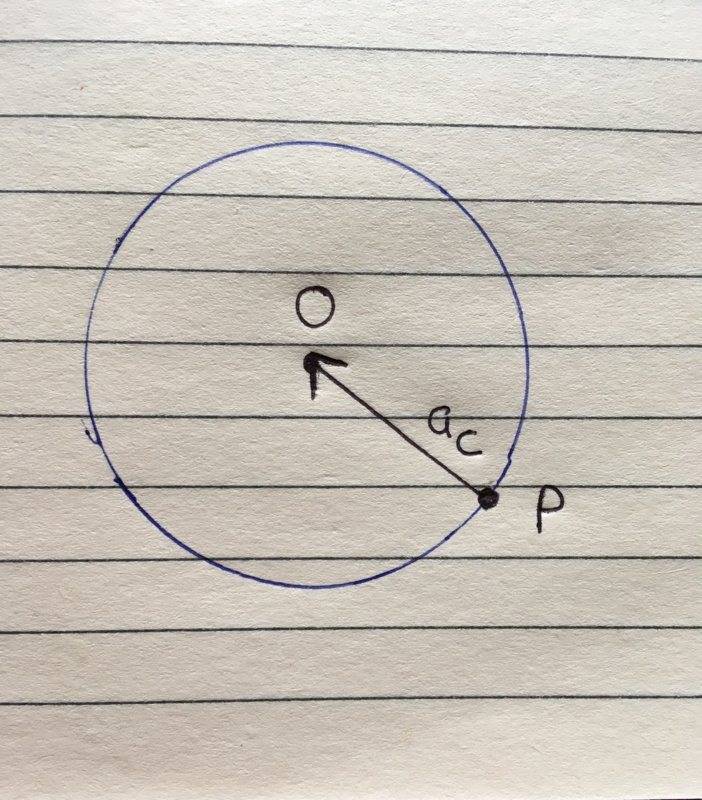
But if centripetal acceleration’s direction of point P were to act horizontally from point towards AB then we won’t get $a_g$ cancelled. How about having a centripetal acceleration acting from P to the point O? In this way we surely going to get a vertical component of centripetal acceleration.

By some simple geometry:

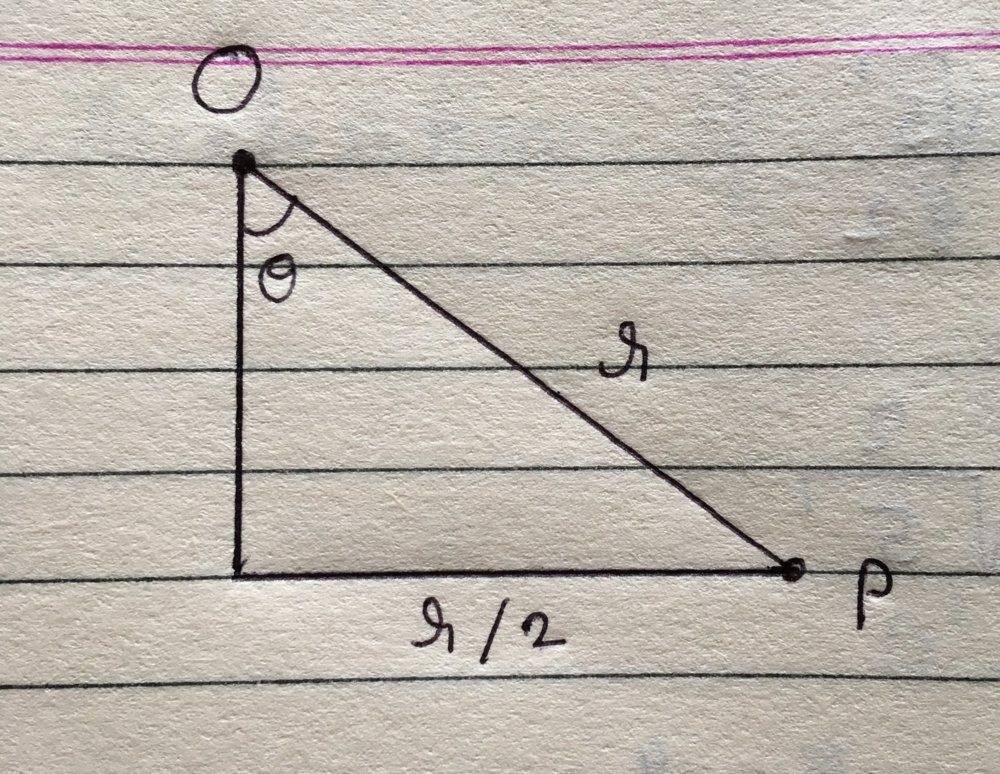
We would get $\theta = \frac{\pi}{6}$. Now, the vertical component of $a_c$ is $a_c \cos \theta = \frac{v^2}{r} \frac{\sqrt 3}{2} = \frac{\sqrt 3 \omega^2 ~r}{2}$. Now for equilibrium we must have $$ a_c \cos \theta = g \\
\frac{\sqrt 3~\omega^2 ~r}{2 } =g \\
\omega ^2 = \frac{2g}{\sqrt 3~r}$$.

Although, I have reached to the correct answer but I suspect the step when I said the centripetal acceleration would act from P towards O.

 

[PeroK]

You're forgetting the normal force from the wire. For equilibrium the combined force of gravity and the normal force must equal the required centripetal force.

 

[Adesh]

You're forgetting the normal force from the wire

Normal force from what? Can you please draw it in my diagram which I have posted in my original post?

 

[PeroK]

Normal force from what? Can you please draw it in my diagram which I have posted in my original post?

Whether the wire is spinning or not, there are two forces acting on the bead. If there were only gravity, then the bead would fall straight to the ground (as though the wire were not there). As the bead falls, the wire forces it to move in the shape of the wire. As there is no friction, this force must be normal to the curve of the wire.

There is no direct centripetal force in this problem. In equilibrium, the centripetal force is the sum of the other two forces: it's the total force in $F = ma$.

 

[etotheipi]

Normal force from what? Can you please draw it in my diagram which I have posted in my original post?

If you can tolerate my crude artistic skills, this is a cross-section of the bead and wire frame, where the blue part is supposed to be the wire frame and the black part the bead. The red arrows are the contact forces.

For any angle other than $\theta = 0$ the normal force is going to have a horizontal component because the plane of contact between the wire and the bead will also no longer be horizontal wrt the lab.

 

[Adesh]

As the bead falls, the wire forces it to move in the shape of the wire. As there is no friction, this force must be normal to the curve of the wire.

Does normal force act towards the Center and when we resolve it the vertical component cancels the gravity and the horizontal component causes it to move along the curve of the wire?

If that is so, then how do we find the magnitude of the normal force ? And how the wire exerts the normal force, is it the two portions of wire on the sides P exert forces on it?

 

[Adesh]

where the blue part is supposed to be the wire frame and the black part the bead.

I think the blue part represents the bead and the black represents the wire.

 

[PeroK]

Does normal force act towards the Center and when we resolve it the vertical component cancels the gravity and the horizontal component causes it to move along the curve of the wire?

If that is so, then how do we find the magnitude of the normal force ? And how the wire exerts the normal force, is it the two portions of wire on the sides P exert forces on it?

The wire is a circle and the normal to a circle is colinear with the radius.

You find the forces the way you always do in an equilibrium problem: balancing forces using $\vec F = m \vec a$.

 

[etotheipi]

Diagram check

 

[Adesh]

Diagram check
View attachment 261472

How to get the magnitude of $\mathbf N$ ?

 

[etotheipi]

How to get the magnitude of $\mathbf N$ ?

You don't really need the magnitude. The bead is at rest vertically so $F_y = N\cos{\theta} - W = ma_y = 0$. Now choose a cylindrical coordinate system with the origin at the centre of rotation of the bead so that $F_r = ma_r = -mr\omega^2$. You also know from the diagram that $F_r = -N\sin{\theta}$. Now you have two equations and can eliminate $N$.

 

[Adesh]

You don't really need the magnitude. The bead is at rest vertically so $F_y = N\cos{\theta} - W = ma_y = 0$. Now choose a polar coordinate system with the origin at the centre of rotation of the bead so that $F_r = ma_r = -mr\omega^2$. You also know from the diagram that $F_r = -N\sin{\theta}$. Now you have two equations and can eliminate $N$.

I have a little confusion here: why $F_{r}$ is equal to $m\omega^2 r$? Beacuse $F_r$ must go from origin O to the point P where the force is acting, hence according to me $F_r = N$.

 

[etotheipi]

I have a little confusion here: why $F_{r}$ is equal to $m\omega^2 r$? Beacuse $F_r$ must go from origin O to the point P where the force is acting, hence according to me $F_r = N$.

A cylindrical coordinate system would be more appropriate in 3D, I've edited my last post. But the same logic still stands, and we don't actually need to use the vertical coordinate (so it's essentially still polar).

I set the origin of this coordinate system at the centre of rotation of the bead. This is not the centre of the sphere traced out by the rotating wire frame!

 

[haruspex]

we won’t get $a_g$ cancelled.

Further to @PeroK's point, the centripetal force would not "cancel" gravity anyway.
Centripetal force is not an applied force. In the present case, gravity and the restraining force from the wire are the applied forces. They have a resultant.
The centripetal force is, by definition, the component (of the resultant of all applied forces) which is normal to the velocity.

 

[Adesh]

Further to @PeroK's point, the centripetal force would not "cancel" gravity anyway.
Centripetal force is not an applied force. In the present case, gravity and the restraining force from the wire are the applied forces. They have a resultant.
The centripetal force is, by definition, the component (of the resultant of all applied forces) which is normal to the velocity.

Oh my God! I never knew this, thank you so much for telling me that. This is what I have understood from your reply:

Centripetal force is just one of those components of the applied force which acts towards the center/axis of rotation, you cannot apply centripetal force, gravity can be applied, tension can be applied, normal force can be applied but not the centripetal force..

I have saved a screenshot of your reply , it was just amazing .

 

[Adesh]

I’m still getting two problems:

1. From the diagram of @etotheipi (that blue ball and black rim diagram, where he made the mistake of calling the blue ball as the wire instead of the bead ) it was quite natural to imagine that normal force existed, but in real life the wire goes through the bead (there is a hole in the bead through which the wire goes) and I’m finding it very hard to imagine how normal force will be exerted in that case.

2. Why I got a right answer when I used $\mathbf N$ as $m~\omega^2 r$ ? Is the magnitude of $\mathbf N$ really the $m\omega ^2 ~r$?

 

[etotheipi]

that blue ball and black rim diagram, where he made the mistake of calling the blue ball as the wire instead of the bead

An unfortunate mistake on my part

it was quite natural to imagine that normal force existed, but in real life the wire goes through the bead (there is a hole in the bead through which the wire goes) and I’m finding it very hard to imagine how normal force will be exerted in that case.

See post #5. Sorry for the colour change!

2. Why I got a right answer when I used $\mathbf N$ as $m~\omega^2 r$ ? Is the magnitude of $\mathbf N$ really the $m\omega ^2 ~r$?

Can you show your work here? I'm not quite sure how you got this part.

 

[Adesh]

Can you show your work here? I'm not quite sure how you got this part.

It is in my original post.

 

[etotheipi]

On the bead, $$\mathbf{N} + m\mathbf{g} = m\mathbf{a} = -mr\omega^2 \mathbf{e}_r$$ $$(N\cos{\theta})\mathbf{e}_z - (N\sin{\theta}) \mathbf{e}_r -mg \mathbf{e}_z = -mr\omega^2 \mathbf{e}_r$$ Then it follows that $N\sin{\theta} = mr\omega^{2}$.

N.B. I'm having a sort of internal crisis about whether to use $\mathbf{v}$ or $\vec{v}$; the latter seems more natural but the former looks cooler...

 

[etotheipi]

The centripetal force is, by definition, the component (of the resultant of all applied forces) which is normal to the velocity.

Just out of interest, a charge moving with $\mathbf{v} = v_x \mathbf{e}_x + v_y \mathbf{e}_y + v_z \mathbf{e}_z$ in a uniform magnetic field ends up with a helical trajectory. If we let $\mathbf{B} = B_x \mathbf{e}_x$, for instance, the force $\mathbf{F} = -qv_z B_x \mathbf{e}_y - qv_y B_x \mathbf{e}_z$ isn't perpendicular to $\mathbf{v}$. I've always considered $\mathbf{F}$ in this context to be a centripetal force, but according to this definition it wouldn't be.

I wondered what you think? Thanks!

 

[Adesh]

If we let B=BxexB=Bxex\mathbf{B} = B_x \mathbf{e}_x, the force F=−qvzBxey−qvyBxezF=−qvzBxey−qvyBxez\mathbf{F} = -qv_z B_x \mathbf{e}_y - qv_y B_x \mathbf{e}_z isn't perpendicular to v

It is indeed perpendicular to $\mathbf v$. Take its dot product with $\mathbf v$ and you going to get zero.

 

[etotheipi]

It is indeed perpendicular to $\mathbf v$. Take its dot product with $\mathbf v$ and you going to get zero.

Ah, you're quite right. I put in a minus sign where it didn't belong! Should be $\mathbf{F} = qv_z B_x \mathbf{e}_y - qv_y B_x \mathbf{e}_z$

 

[archaic]

I've deleted my post. If you've read it, forget it.

 

[etotheipi]

I've deleted my post. If you've read it, forget it.

What was wrong with it? I thought you were just showing that if $\vec{r} = r\hat{r}$, then $\vec{v} = \dot{r}\hat{r} + r\dot{\theta} \hat{\theta}$ and $\vec{a} = (\ddot{r} - r{\dot{\theta}}^2)\hat{r} + (r\ddot{\theta} + 2\dot{r}\dot{\theta})\hat{\theta}$ by deriving and not ignoring the unit vectors?

 

[archaic]

What was wrong with it? I thought you were just showing that if $\vec{r} = r\hat{r}$, then $\vec{v} = \dot{r}\hat{r} + r\dot{\theta} \hat{\theta}$ and $\vec{a} = (\ddot{r} - r{\dot{\theta}}^2)\hat{r} + (r\ddot{\theta} + 2\dot{r}\dot{\theta})\hat{\theta}$ by deriving and not ignoring the unit vectors?

I did not take into account that $\vert \vec u\vert$ might have a non linear function as its argument. :x

 

[archaic]

deriving

french influence?

 

[etotheipi]

I did not take into account that $\vert \vec u\vert$ might have a non linear function as its argument. :x

Slipped right past me too!

french influence?

My maths teacher tends to say 'derive' so I guess it just slipped into my vocabulary, derive something and then anti-derive it... I guess it should really be differentiate but why waste precious time on 3 more whole syllables

 

[Adesh]

I guess it should really be differentiate but why waste precious time on 3 more whole syllables

Are you a conservative (of words)?

 

[etotheipi]

@Adesh one other thing that might be useful is the concept of n-t coordinates. The unit vectors are body fixed and are oriented s.t. the normal unit vector $\mathbf{e}_n$ points toward the instantaneous centre of curvature and the tangential unit vector $\mathbf{e}_t$ points in the same direction as the velocity vector.

Since the centripetal force & centripetal accelerations are by definition those components orthogonal to the velocity, we know that $\mathbf{a}_c = \frac{v^2}{\rho} \mathbf{e}_n$ and by extension $\mathbf{F}_c = m\frac{v^2}{\rho} \mathbf{e}_n$. In the case of planar circular anti-clockwise motion, this coordinate system has nearly the same unit vectors as a polar coordinate system (save for the direction of the normal/radial ones). Whilst if we now consider something like elliptical motion, the centripetal acceleration is no longer in the direction of the $\mathbf{e}_{r}$ unit vector but it is definitely still along the $\mathbf{e}_n$ unit vector direction by definition.

Are you a conservative (of words)?

I guess I'd need to calculate the work I do around a closed path first in order to find out... one sec. let me just run around the garden and check.