SUMMARY
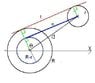
The discussion focuses on finding a direct formula for calculating the direct common tangent of two circles without resorting to the traditional method of deriving separate tangents. The solution involves adjusting the radius of the larger circle by the radius of the smaller circle, allowing for the determination of the tangent angle using the distance between the centers of the circles and the difference in their radii. This method simplifies the process of identifying tangent points on both circles.
PREREQUISITES
- Understanding of basic circle geometry
- Familiarity with tangent lines and their properties
- Knowledge of coordinate geometry
- Ability to manipulate geometric equations
NEXT STEPS
- Study the derivation of tangent lines in circle geometry
- Explore the concept of shrinking and expanding circle radii
- Learn about the geometric properties of tangents from external points
- Investigate the application of trigonometry in circle-related problems
USEFUL FOR
Mathematicians, geometry students, and educators seeking efficient methods for calculating tangents between circles will benefit from this discussion.