member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this problem,

The solution is,
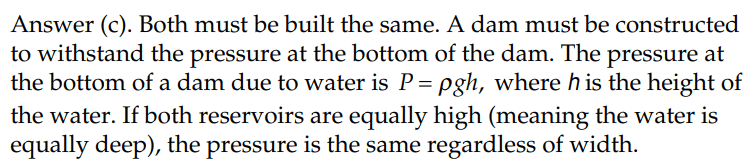
However, I though dams were built to withstand the average force exerted by the water. Therefore, from ##PA = F## a larger width dam would have less force exerted on it due to the greater area so would not have to be as thick (less mass, and thus inertia). Can someone please give me some guidance to come to their way of thinking?
Many thanks!
The solution is,
However, I though dams were built to withstand the average force exerted by the water. Therefore, from ##PA = F## a larger width dam would have less force exerted on it due to the greater area so would not have to be as thick (less mass, and thus inertia). Can someone please give me some guidance to come to their way of thinking?
Many thanks!