SUMMARY
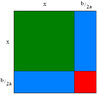
The discussion focuses on completing the square for the quadratic expression \(y = x^2 + 4x + 5\) using algebra tiles. The green square represents \(x^2\), while two blue rectangles represent \(2x\). To complete the square, a red square with side lengths of 2 is added, resulting in the expression \(y = (x + 2)^2 + 1\). This method visually demonstrates the algebraic manipulation required to rewrite the quadratic in vertex form.
PREREQUISITES
- Understanding of quadratic equations and their standard form
- Familiarity with algebra tiles as a visual learning tool
- Knowledge of completing the square technique
- Basic algebraic manipulation skills
NEXT STEPS
- Explore the use of algebra tiles for other quadratic expressions
- Learn about the vertex form of quadratic equations
- Study the graphical interpretation of completing the square
- Investigate the relationship between completing the square and the quadratic formula
USEFUL FOR
Students learning algebra, educators teaching quadratic functions, and anyone interested in visual methods for solving equations.