Complex analysis and complex plane

Thread starter tsopatsopa
Start date Jun 25, 2011
Tags

Analysis Complex Complex analysis Complex plane Plane

In summary, complex analysis is a branch of mathematics that deals with the properties and behavior of complex numbers and functions. It is important as it provides a powerful tool for solving problems in various fields. The complex plane, which is a geometric representation of complex numbers, is closely related to complex analysis and allows for visualization and analysis of complex functions. The basic operations in complex analysis include addition, subtraction, multiplication, and division of complex numbers, as well as other important operations such as taking the complex conjugate and evaluating complex functions. Complex analysis has a wide range of applications in fields such as electromagnetism, fluid dynamics, and quantum mechanics. Some key concepts in complex analysis include analytic functions, contour integration, and the Cauchy integral theorem.

Jun 25, 2011

tsopatsopa

Homework Statement

Let z= x + yi be a complex number.
and f(z) = u + vi a complex function.
As:
u = sinx[itex]\ast[/itex]coshy
v= cosx[itex]\ast[/itex]sinhy

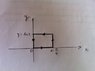
And if z has a trajectory shown in the attached image.
What would be the trajectory of the point (u,v) ?

Physics news on Phys.org

Jun 26, 2011

I like Serena

Homework Helper

MHB

Welcome to PF, tsopatsopa!

Pick a couple of points on the trajectory and plug the numbers into your function?

1. What is complex analysis and why is it important?

Complex analysis is a branch of mathematics that deals with the properties and behavior of complex numbers and functions. It is important because it provides a powerful tool for solving problems in various fields such as physics, engineering, and economics.

2. What is the complex plane and how is it related to complex analysis?

The complex plane is a geometric representation of complex numbers, with the real numbers on the horizontal axis and the imaginary numbers on the vertical axis. It is closely related to complex analysis as it allows us to visualize and analyze complex functions in a simple and intuitive way.

3. What are the basic operations in complex analysis?

The basic operations in complex analysis include addition, subtraction, multiplication, and division of complex numbers. Other important operations include taking the complex conjugate, finding the modulus and argument of a complex number, and evaluating complex functions.

4. What are the main applications of complex analysis?

Complex analysis has a wide range of applications in various fields such as electromagnetism, fluid dynamics, signal processing, and quantum mechanics. It is also used in the study of differential equations and in the development of mathematical models for real-world problems.

5. What are the key concepts in complex analysis?

Some key concepts in complex analysis include analytic functions, Cauchy-Riemann equations, contour integration, residues, and the Cauchy integral theorem. Other important concepts include power series, Laurent series, and the maximum modulus principle.