- #1
kidsasd987
- 143
- 4
I understood the holomorphic condition this way.
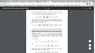
For a vector field
F(x1, x2 . . ., xm) = <y1(x1, x2, x3 . . . , xm), y2(x1, x2, x3 . . . , xm), y3(x1, x2, x3 . . . , xm) . . . ,yn(x1, x2, x3 . . . , xm)>
In a real analysis, its derivative is expressed as a Jacobian matrix because each field component would have a different incremental because the components are independent of each other.However, complex differentiation is just like the case of single real variable differentiation but defined on the complex number set, which imposes a stronger restriction. And this can be generalizd to quaternion, octanion and so on.Is this right?
For a vector field
F(x1, x2 . . ., xm) = <y1(x1, x2, x3 . . . , xm), y2(x1, x2, x3 . . . , xm), y3(x1, x2, x3 . . . , xm) . . . ,yn(x1, x2, x3 . . . , xm)>
In a real analysis, its derivative is expressed as a Jacobian matrix because each field component would have a different incremental because the components are independent of each other.However, complex differentiation is just like the case of single real variable differentiation but defined on the complex number set, which imposes a stronger restriction. And this can be generalizd to quaternion, octanion and so on.Is this right?