Complex Numbers VI: Finding Least Value of |z-2√2-4i|

[Punch]

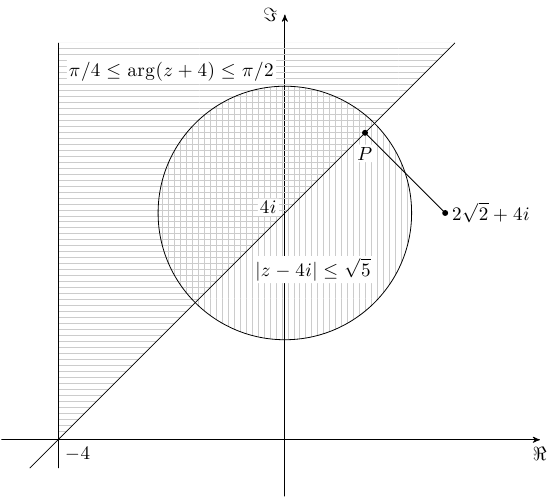
Sketch on an Argand diagram the set of points satisfying both |z-4i|<=\sqrt{5} and \frac{\pi}{4}<=arg(z+4)<=\frac{\pi}{2}.

I have already sketched the 2 loci. The problem lies in the following part.

Hence find the least value of |z-2\sqrt{2}-4i|. Find, in exact form, the complex number z_1 represented by the point P that gives this least value.

 

[Evgeny.Makarov]

Hence find the least value of |z-2\sqrt{2}-4i|.

Over which set of z? The intersection defined in the first part? It seems that you need to find the shortest distance from a point to a semi-disk.

Why don't you wrap the $$...$$ tags around your formulas?

 

[Punch]

Over which set of z? The intersection defined in the first part? It seems that you need to find the shortest distance from a point to a semi-disk.

Why don't you wrap the \(z_1\) tags around your formulas?

Yes, how do I then find the complex number $$z_1$$ in the following part?

I tried using the latex but they didnt seem to work

 

[Evgeny.Makarov]

Yes, how do I then find the complex number $$z_1$$ in the following part?

See the following picture.

I tried using the latex but they didnt seem to work

Type $$\frac{\pi}{4}\le\arg(z+4)\le\frac{\pi}{2}$$ to get $$\frac{\pi}{4}\le\arg(z+4)\le\frac{\pi}{2}$$.

 

[CellCoree]

To find the least value of |z-2\sqrt{2}-4i|, we need to find the closest point to the origin on the locus |z-2\sqrt{2}-4i|. This can be done by setting z=x+yi and using the distance formula.

Distance formula: d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}

Substituting z=x+yi and the given values of 2√2 and 4i, we get:

d=\sqrt{(x-2√2)^2+(y-4)^2}

Since we want to find the closest point to the origin, we can set x=0 and y=0:

d=\sqrt{(0-2√2)^2+(0-4)^2}

d=\sqrt{4+16}=√20=2√5

Therefore, the least value of |z-2√2-4i| is 2√5.

To find the exact complex number z_1 represented by the point P that gives this least value, we can substitute the values of x and y into z=x+yi:

z_1=0+0i=0

Therefore, the complex number z_1 is 0.

On the Argand diagram, this point would lie on the x-axis, 2√2 units to the left of the origin. This satisfies both loci and gives the least value of |z-2√2-4i|.