- #1
Delmache
- 3
- 0
Hi everyone,
I'm french, so sorry for my bad english.
I have a problem to compute the damping as a function of frequency. In fact, I plot the transfer function between the input (which is a force applied bu a hammer) and the output (which is an acceleration). Therefore, I can analyse the mode of the structure... I want to know the damping of the first mode, so I have used the "-3dB method". But I need to justify the value from the "-3dB method". What I'd like to do, is to compute the damping over the frequency (between 0-200 Hz). As I said before, my transfer function is the following :
H* = Output/Input = a/F
As you know, the stiffness is computed by :
K = F/delta(d)
What I do is that I use the transfer function to compute the damping, so I transform the equation of the transfer function as following :
1/H* = F/a
F/(a/jw)² = F/d (as you know d=a/(jw)²
So, 1/H* = -(w²*F)/a
Therefore, K* = -w²/H*
Then, I compute "eta" which is the damping by the following equation :
eta = Imaginary(K)/Real(K)
But when I do these calculations, I find very strange results. Balow, I show you an example of what I find :
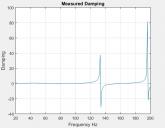
First, I don't find the same value of damping obtained from the "-3dB method".
Second, I find incoherent values of damping (>1 or <1...). I can't explain this curve and why my computation doesn't work. What do I do wrong ?
Or, is there an other method to compute the damping as a function of frequency ?
Thank you very much for your help.B.D
I'm french, so sorry for my bad english.
I have a problem to compute the damping as a function of frequency. In fact, I plot the transfer function between the input (which is a force applied bu a hammer) and the output (which is an acceleration). Therefore, I can analyse the mode of the structure... I want to know the damping of the first mode, so I have used the "-3dB method". But I need to justify the value from the "-3dB method". What I'd like to do, is to compute the damping over the frequency (between 0-200 Hz). As I said before, my transfer function is the following :
H* = Output/Input = a/F
As you know, the stiffness is computed by :
K = F/delta(d)
What I do is that I use the transfer function to compute the damping, so I transform the equation of the transfer function as following :
1/H* = F/a
F/(a/jw)² = F/d (as you know d=a/(jw)²
So, 1/H* = -(w²*F)/a
Therefore, K* = -w²/H*
Then, I compute "eta" which is the damping by the following equation :
eta = Imaginary(K)/Real(K)
But when I do these calculations, I find very strange results. Balow, I show you an example of what I find :
First, I don't find the same value of damping obtained from the "-3dB method".
Second, I find incoherent values of damping (>1 or <1...). I can't explain this curve and why my computation doesn't work. What do I do wrong ?
Or, is there an other method to compute the damping as a function of frequency ?
Thank you very much for your help.B.D
Last edited: