- #1
zenterix
- 480
- 70
- Homework Statement
- I've seen the word "resonance" appear in different scenarios in a mass-spring-dashpot system.
Does resonance refer specifically only to a setup involving a simple harmonic oscillator or does it also have meaning in a system that has damping?
- Relevant Equations
- Here are three places where I saw the word "resonance".
1) "Undamped system is forced at the same frequency as one of its natural frequencies."
Consider the 2nd order differential equation
$$\ddot{x}+\omega_0^2x=F_0\cos{\omega t}\tag{1}$$
which models a mass attached to a spring (attached to a wall) with spring constant ##k## and ##\omega_0=\sqrt{\frac{k}{m}}##.
A particular solution is
$$\frac{F_0\cos{(\omega t)}}{\omega_0^2-\omega^2}\tag{2}$$
if ##\omega_0\neq \omega## and
$$\frac{F_0 t\sin{(\omega_0 t)}}{2\omega_0}\tag{3}$$
when ##\omega_0=\omega##.
The latter case is called resonance, and is characterized by an amplitude of oscillation that grows in time.
This is the case of a pendulum or a swing in which there is a force that is synchronized with the natural frequency such that the force is zero when the amplitude is at its peaks and acts to "push" the pendulum or swing with increasing magnitude towards the equilibrium point, and once that equilibrium point is reached the force continues to push but with decreasing intensity until it reaches zero again at the next peak.
This timing makes it so that each successive peak has a greater amplitude.
One doubt I have is about what it means that an undamped system has multiple natural frequencies.
2) If we consider a general mass-spring-dashpot system the equation that describes the system is
$$m\ddot{x}+c\dot{x}+kx=F_0\cos{\omega t}\tag{4}$$
The steady-state solution is
$$\frac{F_0}{\sqrt{(k-\omega^2m)^2+\omega^2c^2}}\cos{(\omega t-\phi)}\tag{6}$$
The amplitude of the steady state solution is
$$A=\frac{F_0}{\sqrt{(k-\omega^2m)^2+\omega^2c^2}}\tag{7}$$
Of this expression, Simmons book "Differential Equations with Applications and Historical Notes" says
This case does not involve a growing amplitude, but rather simply a large amplitude. It seems that one could make the amplitude arbitrarily large if we are allowed to tweak any of the parameters.
For a given set of parameters except ##\omega##, there seems to be a maximum amplitude and this is shown in part 3 below.
3) I found a third use of the term resonance in the following problem.
If we consider (7) as a function of ##\omega## and try to find a critical point, we find
$$\omega=\sqrt{\frac{2km-c^2}{2m^2}}=\sqrt{\frac{k}{m}-\frac{c^2}{2m^2}}\tag{8}$$
which is the resonance frequency. Compared to the natural frequency
$$\sqrt{\frac{k}{m}-\frac{c^2}{4m^2}}\tag{9}$$
we see that the resonance frequency is smaller.
The amplitude for this frequency is
$$\frac{2F_0m}{\sqrt{c^2(4km-c^2)}}\tag{10}$$
Once more, the amplitude does not grow in time, but we can make it arbitrarily large at the resonance frequency by tweaking the parameters.
In particular, for a damped system, the closer we are to critical damping (ie, the closer ##4km-c^2## is to zero) the larger the amplitude.
Here is an example of this latter case
$$\ddot{x}+\dot{x}+2x=\cos{(\omega t)}\tag{11}$$
Here is a plot of amplitude as a function of ##\omega##
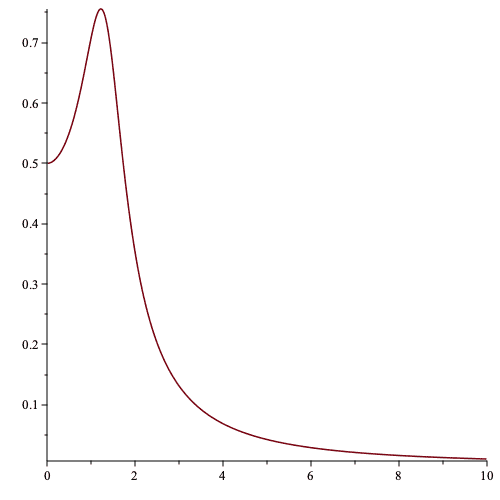
In summary, I showed three cases.
2) and 3) actually seem to be the same thing.
I was under the impression that the concept of resonance was only case 1.
However, resonance frequency seems to be the frequency at which amplitude is maximized in a general 2nd order linear differential equation with constant coefficients and sinusoidal input.
One further comment.
If there is no external sinusoidal input, then the system has a steady state of zero. In this case, it does not seem there is any resonance frequency.
However, if there is sinusoidal input, then the amplitude of the steady-state has a max relative to the input angular frequency.
Consider the 2nd order differential equation
$$\ddot{x}+\omega_0^2x=F_0\cos{\omega t}\tag{1}$$
which models a mass attached to a spring (attached to a wall) with spring constant ##k## and ##\omega_0=\sqrt{\frac{k}{m}}##.
A particular solution is
$$\frac{F_0\cos{(\omega t)}}{\omega_0^2-\omega^2}\tag{2}$$
if ##\omega_0\neq \omega## and
$$\frac{F_0 t\sin{(\omega_0 t)}}{2\omega_0}\tag{3}$$
when ##\omega_0=\omega##.
The latter case is called resonance, and is characterized by an amplitude of oscillation that grows in time.
This is the case of a pendulum or a swing in which there is a force that is synchronized with the natural frequency such that the force is zero when the amplitude is at its peaks and acts to "push" the pendulum or swing with increasing magnitude towards the equilibrium point, and once that equilibrium point is reached the force continues to push but with decreasing intensity until it reaches zero again at the next peak.
This timing makes it so that each successive peak has a greater amplitude.
One doubt I have is about what it means that an undamped system has multiple natural frequencies.
2) If we consider a general mass-spring-dashpot system the equation that describes the system is
$$m\ddot{x}+c\dot{x}+kx=F_0\cos{\omega t}\tag{4}$$
The steady-state solution is
$$\frac{F_0}{\sqrt{(k-\omega^2m)^2+\omega^2c^2}}\cos{(\omega t-\phi)}\tag{6}$$
The amplitude of the steady state solution is
$$A=\frac{F_0}{\sqrt{(k-\omega^2m)^2+\omega^2c^2}}\tag{7}$$
Of this expression, Simmons book "Differential Equations with Applications and Historical Notes" says
This case does not involve a growing amplitude, but rather simply a large amplitude. It seems that one could make the amplitude arbitrarily large if we are allowed to tweak any of the parameters.
For a given set of parameters except ##\omega##, there seems to be a maximum amplitude and this is shown in part 3 below.
3) I found a third use of the term resonance in the following problem.
If we consider (7) as a function of ##\omega## and try to find a critical point, we find
$$\omega=\sqrt{\frac{2km-c^2}{2m^2}}=\sqrt{\frac{k}{m}-\frac{c^2}{2m^2}}\tag{8}$$
which is the resonance frequency. Compared to the natural frequency
$$\sqrt{\frac{k}{m}-\frac{c^2}{4m^2}}\tag{9}$$
we see that the resonance frequency is smaller.
The amplitude for this frequency is
$$\frac{2F_0m}{\sqrt{c^2(4km-c^2)}}\tag{10}$$
Once more, the amplitude does not grow in time, but we can make it arbitrarily large at the resonance frequency by tweaking the parameters.
In particular, for a damped system, the closer we are to critical damping (ie, the closer ##4km-c^2## is to zero) the larger the amplitude.
Here is an example of this latter case
$$\ddot{x}+\dot{x}+2x=\cos{(\omega t)}\tag{11}$$
Here is a plot of amplitude as a function of ##\omega##
In summary, I showed three cases.
2) and 3) actually seem to be the same thing.
I was under the impression that the concept of resonance was only case 1.
However, resonance frequency seems to be the frequency at which amplitude is maximized in a general 2nd order linear differential equation with constant coefficients and sinusoidal input.
One further comment.
If there is no external sinusoidal input, then the system has a steady state of zero. In this case, it does not seem there is any resonance frequency.
However, if there is sinusoidal input, then the amplitude of the steady-state has a max relative to the input angular frequency.
Last edited:
. Properly naming disastrous physical phenomena since 2014. 
