Compute damping as a function of frequency

[Delmache]

Hi everyone,

I'm french, so sorry for my bad english.

I have a problem to compute the damping as a function of frequency. In fact, I plot the transfer function between the input (which is a force applied bu a hammer) and the output (which is an acceleration). Therefore, I can analyse the mode of the structure... I want to know the damping of the first mode, so I have used the "-3dB method". But I need to justify the value from the "-3dB method". What I'd like to do, is to compute the damping over the frequency (between 0-200 Hz). As I said before, my transfer function is the following :

H* = Output/Input = a/F

As you know, the stiffness is computed by :

K = F/delta(d)

What I do is that I use the transfer function to compute the damping, so I transform the equation of the transfer function as following :

1/H* = F/a

F/(a/jw)² = F/d (as you know d=a/(jw)²

So, 1/H* = -(w²*F)/a

Therefore, K* = -w²/H*

Then, I compute "eta" which is the damping by the following equation :

eta = Imaginary(K)/Real(K)

But when I do these calculations, I find very strange results. Balow, I show you an example of what I find :

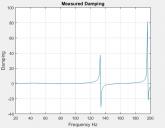
First, I don't find the same value of damping obtained from the "-3dB method".
Second, I find incoherent values of damping (>1 or <1...). I can't explain this curve and why my computation doesn't work. What do I do wrong ?
Or, is there an other method to compute the damping as a function of frequency ?
Thank you very much for your help.B.D

 

[Delmache]

Hi

Anyone can help me ?

Thanks
B.D

 

[Delmache]

Hi,

I am looking for the relation between the stiffness, the young's modulus and the loss factor. I think that's K = E(1+i*η), but I'm not sure of that. Can someone confirm that equation ? Because I need to justify the following equation : η = imaginary(K) / real(K).
Thanks a lot,
B.D