Conformal Mapping for Transforming Regions: Finding a Function

[MaxJasper]

Hello folks,

I am trying to find a conformal mapping transform function that maps the following region in z-plane into interior of a unit circle in w-plane:

$|z-i|<\sqrt{2}\text{ ...AND... }|z+i|<\sqrt{2}$

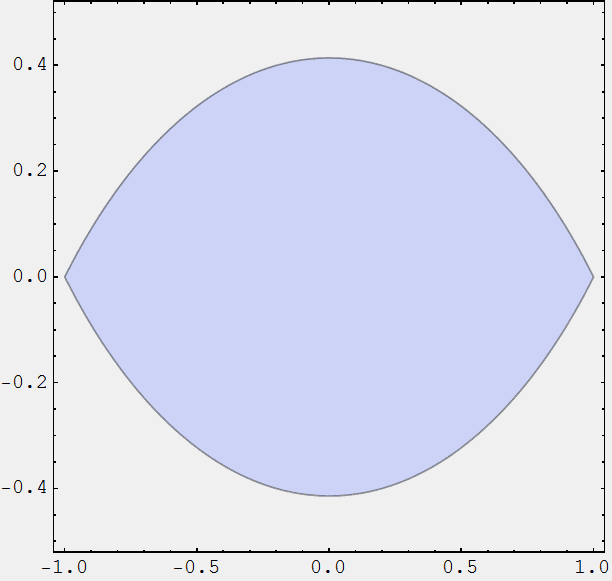
Many thanks in advance for help & clues.
Max.

 

[meldraft]

The most general way to calculate a conformal mapping is a Schwarz-Christoffel mapping. This integral however can't be solved analytically in most cases.

You can split the domain in two along the imaginary axis and try to map the semi circle into one half, and then mirror it to get the other half. I know that you can get that half-shape through ζ=z^2 if you original domain is a square. You can see it here (p. 246):

http://www.math.umn.edu/~olver/pd_/cm.pdf

All you need then is a mapping from unit disk to unit square. One way you could (maybe) do this is by starting with the half-disk, tranform it to a half-plane, and then fold it to a square using a Schwarz-Christoffel mapping. I think that this case can be solved analytically. You then mirror your domain along the imaginary axis and you're done. This is easier said than done of course, but that is the nature of conformal mappings