Confused on the power through a Capacitor formula help

[nchin]

I know that the energy stored in a capacitor is U = 1/2 CV². but the power through it? I have in my notes that the power is the derivative of U.

so for example the energy is 26 Joules so the derivative of 26 J? doesn't make sense cause 26 is a constant.

help please!

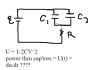
i attached a picture of the problem. i first find the C equivalent.

oops! there's actually a switch on the top of the circuit! which closes at t = 0

 

[gneill]

Can you find an expression for the potential across the equivalent capacitance with respect to time? How about the stored energy? This expression should be differentiable w.r.t. time...

 

[nchin]

Can you find an expression for the potential across the equivalent capacitance with respect to time? How about the stored energy? This expression should be differentiable w.r.t. time...

potential across is C = QV --> V(t) = C/Q(t). is that it?

 

[gneill]

potential across is C = QV --> V(t) = C/Q(t). is that it?

No. C is capacitance, not potential. C = QV is not a correct formula. And Q(t) does not provide any information about how the charge Q changes over time.

What is the expression for the voltage across the capacitance with respect to time for the given circuit? Hint: it involves an exponential function with a time constant.

 

[Nickie]

Hi there,

I understand your confusion about the power through a capacitor. The formula for power through a capacitor is P = dU/dt, where U is the energy stored in the capacitor and t is time. This formula represents the rate at which energy is being transferred to or from the capacitor.

In the example you provided, you have the energy stored in the capacitor (U) and you are trying to find the power (P) at a specific time (t=0). In this case, the derivative of 26 J doesn't make sense because 26 is a constant value and not a function of time.

However, if you have a switch in the circuit that closes at t=0, then the energy stored in the capacitor will start changing over time. In this case, you would need to use the formula P = dU/dt at different time points to find the power at each time point.

I hope this helps clarify things for you. Remember, power through a capacitor is the rate at which energy is being transferred, so it will depend on the change in energy over time.

Best of luck with your studies!