Confusing Venn Diagram problem

In summary, a group of 50 Grade 6 students were surveyed on their favorite types of kid-friendly content on Youtube. Out of the 50 students, 17 liked Gaming Videos only, 6 liked Gaming Videos and How-To videos, 2 liked How-To and Comedy videos, 6 liked Gaming and Comedy, 5 liked Comedy videos only, 1 liked How-To videos only, 8 liked all three, and 4 chose none of the three. The diagram shown by the user is correct, but when adding all the numbers inside the diagram, the sum is 49 instead of 50. This is most likely an error made by the person who constructed the problem.
  • #1
TheDoctor
8
0
Hi there, I have this performance task on Math and I'm struggling with this Venn diagram problem.

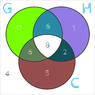
50 Grade 6 students were surveyed on their favorite types of kid-friendly content on Youtube. 17 liked Gaming Videos only, 6 liked Gaming Videos and How-To videos, 2 liked How-To and Comedy videos, 6 liked Gaming and Comedy, 5 liked Comedy videos only, 1 liked How-To videos only, 8 liked all three, and 4 chose none of the three.

I have done my own version of the diagram, which is shown here:

View attachment 7006

I don't know if I'm right or not though so I'd appreciate any help.

Thanks in advance.
 

Attachments

  • venn01.png
    venn01.png
    15.6 KB · Views: 101
Last edited by a moderator:
Mathematics news on Phys.org
  • #2
Hello and welcome to MHB, TheDoctor! (Wave)

Your diagram looks correct to me. (Yes)
 
  • #3
MarkFL said:
Hello and welcome to MHB, TheDoctor! (Wave)

Your diagram looks correct to me. (Yes)

Thanks so much! Though, when I add all the numbers inside the diagram, 49 is the sum, but it's supposed to be 50. 50-49=1, will I add the 1 to the 4 who didn't like any of the three?
 
  • #4
TheDoctor said:
Thanks so much! Though, when I add all the numbers inside the diagram, 49 is the sum, but it's supposed to be 50. 50-49=1, will I add the 1 to the 4 who didn't like any of the three?

I would say the error was made by whomever constructed the problem, not you. :D
 
  • #5
MarkFL said:
I would say the error was made by whomever constructed the problem, not you. :D

Haha, it does get quite confusing so that makes sense. Thanks again!
 

FAQ: Confusing Venn Diagram problem

What is a Venn diagram and how is it used?

A Venn diagram is a visual representation of the relationships between different sets of data. It is used to illustrate the similarities and differences between two or more groups or concepts. The overlapping areas of the circles in a Venn diagram show the common elements between the groups, while the non-overlapping areas represent the unique elements of each group.

Why are Venn diagrams sometimes confusing?

Venn diagrams can be confusing because they require careful analysis and interpretation. In some cases, the overlapping areas may not be clearly defined, making it difficult to determine which elements belong to which groups. Additionally, Venn diagrams can become complex when more than two groups are involved, making it challenging to accurately represent all the relationships between the data sets.

Can you provide an example of a confusing Venn diagram problem?

A common confusing Venn diagram problem may involve three overlapping circles representing different types of animals. The circles may be labeled "mammals," "birds," and "reptiles." The problem may then ask the student to determine which animals are both mammals and birds, but not reptiles. This can be challenging because some animals may fit into multiple categories, making it difficult to determine their placement in the diagram.

How can I solve a confusing Venn diagram problem?

The key to solving a confusing Venn diagram problem is to carefully analyze the information provided and to visually break down the diagram into smaller, more manageable parts. Start by identifying the common elements in the overlapping areas and then work your way out to the unique elements in each group. It can also be helpful to use a different color or shading for each group to make the diagram easier to understand.

Are there any tips for creating a clear and easy-to-understand Venn diagram?

To create a clear and easy-to-understand Venn diagram, it is important to keep the number of groups to a minimum, ideally no more than three. Use clear, concise labels for each group and make sure the overlapping areas are clearly defined. It can also be helpful to use consistent shapes and sizes for the circles to avoid confusion. Lastly, take your time and double-check your work to ensure accuracy.

Similar threads

MHB Draw a venn diagram and include the given information
Replies
5
Views
2K
MHB Venn Diagram Question: How many whales were surveyed?
Replies
7
Views
3K
MHB Noelia's question at Yahoo Answers regarding use of a Venn diagram
Replies
1
Views
1K
MHB Venn Diagram Problem: Tipping Survey Results
Replies
1
Views
2K
MHB Why Do Some Students Appear to Be Double-Counted in Math Enrollment Figures?
Replies
4
Views
12K
I Can Angular Velocity Accurately Control Ragdoll Limbs in Game Physics?
Replies
5
Views
2K
MHB Venn Diagram II: Check Answers & Understand Relationships
Replies
11
Views
3K
B Validating Darts Tournament Skill Levels: A Non-Intrusive Approach
Replies
4
Views
1K
MHB Normal Approximation Problem Solving
Replies
4
Views
3K
Can Venn diagrams resemble Cantor sets with infinitely many sets?
Replies
1
Views
4K

Hot Threads

Recent Insights

Back
Top