Hieu
- 2
- 0
1. The problem statement, all variables, and given/known data
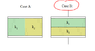
A parallel-plate capacitor has the space between the plates filled with to slabs of dielectric, one with constant K1, & one constant K2. each slab has thickness d⁄2, where d is plate separation, show the capacitance is?
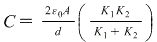
C=Q/V
E=Q/(ε0.A)

V=Q/(4πε0.r)
I consider the conductor as 2 different conductors with different slabs of the dielectric. I think that is not a bad idea to find the answer, but my result is different from the answer, maybe it is wrong somewhere. Can you guys help me? Here is my solution.

A parallel-plate capacitor has the space between the plates filled with to slabs of dielectric, one with constant K1, & one constant K2. each slab has thickness d⁄2, where d is plate separation, show the capacitance is?
Homework Equations
C=Q/V
E=Q/(ε0.A)
V=Q/(4πε0.r)
The Attempt at a Solution
I consider the conductor as 2 different conductors with different slabs of the dielectric. I think that is not a bad idea to find the answer, but my result is different from the answer, maybe it is wrong somewhere. Can you guys help me? Here is my solution.