ARoyC
- 56
- 11
Hi. I am not being able to understand how we are getting the following spectral decomposition. It would be great if someone can explain it to me. Thank you in advance.
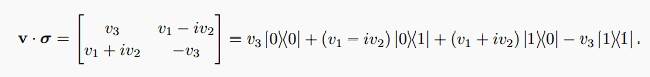
The discussion revolves around the spectral decomposition of an operator in quantum mechanics, specifically addressing the formulation and interpretation of the equation representing the operator in terms of its matrix elements. Participants seek clarification on the validity and derivation of the spectral decomposition, as well as the relationship between operators and their matrix representations.
There is no consensus on the initial equation presented, with some participants contesting its validity and others providing corrections. The discussion remains unresolved regarding the interpretation of the spectral decomposition and the clarity of the initial claims.
Participants reference the completeness relation and the properties of orthonormal bases, but there are unresolved assumptions regarding the definitions and context of the operator and its matrix elements.
Oh! Then we can go to the LHS of the equation from the RHS. Can't we do the reverse?vanhees71 said:It's simply a non-sensical equation. On the one side you write down a matrix, depicting matrix elements of an operator and on the other the operator itself. Correct is
$$\hat{A}=v_3 |0 \rangle \langle 0| + (v_1-\mathrm{i} v_2) |0 \rangle \langle 1| + (v_1+\mathrm{i} v_2) |1 \rangle \langle 0| - v_3 |1 \rangle \langle 1|.$$
The matrix elements in your matrix are then taken with respect to the basis ##(|0 \rangle,|1 \rangle)##.
$$(A_{jk})=\langle j|\hat{A}|k \rangle, \quad j,k \in \{0,1 \}.$$
To see this, simply use ##\langle j|k \rangle=\delta_{jk}##. Then you get, e.g.,
$$A_{01}=\langle 0|\hat{A}|1 \rangle=v_1-\mathrm{i} v_2.$$
How are we getting the very first equality that is A = Σ|j><j|A|k><k| ?vanhees71 said:Sure:
$$\hat{A}=\sum_{j,k} |j \rangle \langle j|\hat{A}|k \rangle \langle k| = \sum_{jk} A_{jk} |j \rangle \langle k|.$$
The mapping from operators to matrix elements with respect to a complete orthonormal system is one-to-one. As very many formal manipulations in QT, it's just using the completeness relation,
$$\sum_j |j \rangle \langle j|=\hat{1}.$$
Oh, okay, thanks a lot!Haborix said:$$\hat{A}=\hat{1}\hat{A}\hat{1}=\left(\sum_{j} |j \rangle \langle j|\right)\hat{A}\left(\sum_{k} |k \rangle \langle k|\right)=\sum_{j,k} |j \rangle \langle j|\hat{A}|k \rangle \langle k| = \sum_{jk} A_{jk} |j \rangle \langle k|.$$