Conservation of linear momentum in RH relations

[GeologistInDisguise]

TL;DR

How is the pictured equation a conservation of momentum equation and what does pressure have to do with it?

I am trying to follow a derivation of the Rankine-Hugoniot equations in a paper by Peter Krehl titled:

The classical Rankine-Hugoniot jump conditions, an important cornerstone of modern shock wave physics: ideal assumptions vs. reality

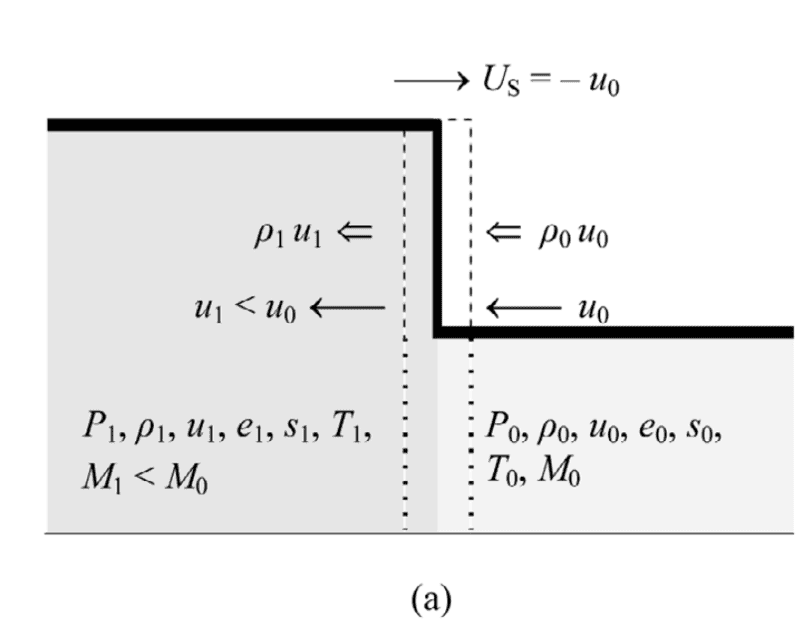
This paper talks about the RH equations which relate kinematic properties to thermodynamic ones when a shock is transiting a material. See photo above for an illustration. In section 2.2.2 when discussing this relation in terms of Lagrangian coordinates, equation 4a is introduced and described as conservation of linear momentum:

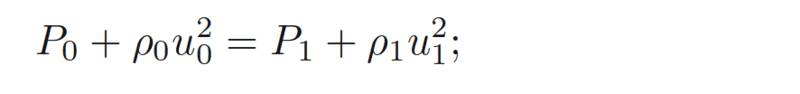
Where P is pressure, rho is density, u is particle velocity, 0 indicates downstream or preshock and 1 indicates upstream or post shock.

While the units do make sense, how is this conservation of momentum? if momentum is m*v, I suppose you could divide by volume to replace mass with density, but then why is velocity squared? And why is pressure being added?

I understand pressure is force/area and also that force is the change in momentum with time. I am guessing this has something to do with it but I am not getting anything that would give me a squared velocity. Obviously if I integrate my mass normalized momentum equation with respect to time, that would give me a velocity squared. But why would I do that?

 

[Frabjous]

ΔP is a force which changes momentum
ρu² is the amount of momentum that is flowing into/out of the box (think m=ρuAΔt)
the AΔt is also attached to the pressures, so it cancels out

 

[GeologistInDisguise]

ΔP is a force which changes momentum
ρu² is the amount of momentum that is flowing into/out of the box (think m=ρuAΔt)
the AΔt is also attached to the pressures, so it cancels out

I think that makes sense, but why then is velocity squared?

 

[Frabjous]

I think that makes sense, but why then is velocity squared?

The “mass” has a velocity in it. You then have to multiply it by velocity to get momentum.

 

[GeologistInDisguise]

The “mass” has a velocity in it. You then have to multiply it by velocity to get momentum.

Oh, in your previous comment was m mass or momentum? I assumed you meant it was momentum since we were using P for pressure already but I think this makes more sense if you did actually mean mass.

 

[Baluncore]

Particle KE = ½·m·v² ≈ absolute temperature.
(speed of sound)² ≈ T_abs
The speed of sound is a direct function of √T_abs only.
Temperature is an indirect function of pressure.

 

[GeologistInDisguise]

Particle KE = ½·m·v² ≈ absolute temperature.
(speed of sound)² ≈ T_abs
The speed of sound is a direct function of √T_abs only.
Temperature is an indirect function of pressure.

This is an interesting point but I am not seeing how it is relevant to the question posted about conservation of momentum?

 

[Frabjous]

Oh, in your previous comment was m mass or momentum? I assumed you meant it was momentum since we were using P for pressure already but I think this makes more sense if you did actually mean mass.

I meant mass.
The equation holds in the reference frame where the shock velocity is zero. So there is a discrepancy between the picture and the equation. I believe the picture should have U_s=0.
There are several versions of the equation. Which one is useful depends on the application.