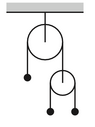
SUMMARY
The discussion centers on the application of the conservation of string principle in a physics problem involving a symmetric sub-pulley system. Participants emphasize the importance of establishing equations that relate the lengths of string sections to the heights of the masses involved. Key equations include the relationship between the vertical positions of the masses and the center of the pulley, leading to the conclusion that the acceleration of the left mass is the negative average of the accelerations of the right two masses. The discussion highlights the necessity of differentiating these relationships to derive velocity and acceleration equations.
PREREQUISITES
- Understanding of conservation of string principles in mechanics
- Familiarity with basic pulley systems and their dynamics
- Knowledge of differentiation in calculus
- Ability to set up and solve equations involving multiple variables
NEXT STEPS
- Study the mechanics of pulley systems, focusing on symmetric configurations
- Learn how to apply conservation laws in dynamic systems
- Practice differentiation techniques relevant to physics problems
- Explore examples of conservation of string problems in classical mechanics
USEFUL FOR
Students studying physics, particularly those focusing on mechanics and dynamics, as well as educators seeking to enhance their understanding of pulley systems and conservation principles.