Kushal Chakrabarti
- 4
- 5
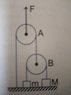
1. The problem: Two blocks of mass m=5kg and M= 10kg are connected by a string passing over a pulley B. Another string connects pulley B to the floor and passes over pulley A. An upward force F is applied at the centre of pulley A. Both pulleys are massless. Find acceleration of the blocks if F is:
a) 100N, b) 300N, c) 500N
Take g=10 ms-2
I have attached an image of the problem.
Attempt at a solution:
Well I drew an FBD in the frame of pulley A, thus using a downward pseudo force. Also, I found using constraint equations that F=4T, where T is the tension in the thread joining the two masses. Thus it gave me two equations ( one for each mass) but solving them, I found out that both the accelerations are turning out to be negative. Where did I go wrong?
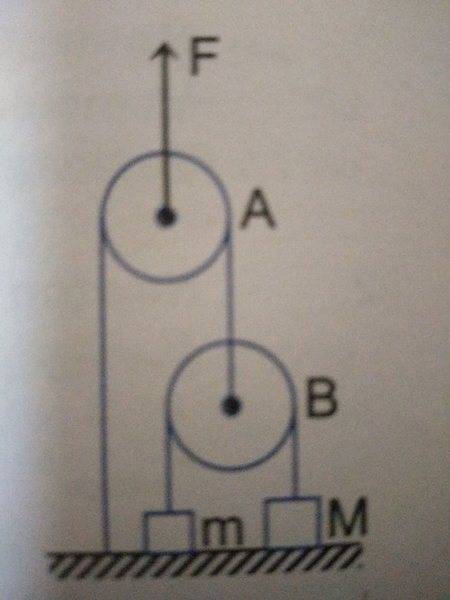
a) 100N, b) 300N, c) 500N
Take g=10 ms-2
I have attached an image of the problem.
Attempt at a solution:
Well I drew an FBD in the frame of pulley A, thus using a downward pseudo force. Also, I found using constraint equations that F=4T, where T is the tension in the thread joining the two masses. Thus it gave me two equations ( one for each mass) but solving them, I found out that both the accelerations are turning out to be negative. Where did I go wrong?